Derandomisation and Randomised Rounding
Derandomisation
-
Sometimes it is possible to “derandomise” a randomised algorithm
Arandand obtain a deterministic algorithmAdet. -
The performance of Adet is the same as the expected performance of Arand.
-
When successful, we can use randomisation at no extra cost!
(except a polynomial running time overhead).
-
Different methods for derandomisation.
-
Can be very complicated (pseudo-random generators).
-
Can be relatively simple (conditional expectations).
-
-
Algorithm: For each variable xi, set xi to 1 with probability 1/2 and to 0 with probability 1/2.
-
Algorithm: Set variable xi to 1 or 0 deterministically, and the remaining variables to 1 with probability 1/2 and to 0 with probability 1/2, as before.
-
To maximise the expected value W of the algorithm.
-
If 𝑊 is the number of clauses satisfied then we have:
𝔼[𝑊] = 𝔼[𝑊|𝑥 ←1]⋅Pr[𝑥 ←1]+𝔼[𝑊|𝑥 ←0]⋅Pr[𝑥 ←0] = 1/2 (𝔼[𝑊|𝑥 ←1] * +𝔼[𝑊|𝑥 ←0])
-
We set x1 to 1 if 𝔼[𝑊|𝑥1 ← 1] ≥ 𝔼[𝑊|𝑥1 ← 0] and to 0 otherwise.
-
Generally, if b1 is picked to maximise the conditional expectation, it holds that: 𝔼[𝑊|𝑥 ←𝑏 ]≥𝔼[𝑊]
Applying this to all variables
-
Assume that we have set variables x1, …, xi to b1, … bi this way.
-
We set xi+1 to 1 if this holds and to 0 otherwise.
𝔼[𝑊|𝑥1 ← 𝑏1,𝑥2 ← 𝑏2,…,𝑥i ← 𝑏i,𝑥i+1 ← 1]≥ 𝔼[𝑊|𝑥1 ← 𝑏1,𝑥2 ← 𝑏2,…,𝑥i ← 𝑏i, 𝑥i+1 ← 0]
-
Again, if bi+1 is picked to maximise the conditional expectation, it holds that:
𝔼[𝑊|𝑥1 ← 𝑏1,𝑥2 ← 𝑏2,…,𝑥i ← 𝑏i,𝑥i+1 ← 𝑏i+1] ≥ 𝔼[𝑊]
In the end
-
In the end we have set all variables deterministically (去随机化).
-
We have 𝔼[𝑊|𝑥1 ← 𝑏1,𝑥2 ← 𝑏2,…,𝑥i ← 𝑏i,𝑥i+1 ← 𝑏i+1] ≥ 𝔼[𝑊]
-
We know that E[W] ≥ 1/2 * OPT
-
We have devised a deterministic 2-approximation algorithm.
-
Is it polynomial-time? Yes
Computing the expectations
- We have to be able to compute the conditional expectations in polynomial time.
𝔼[𝑊|𝑥1 ← 𝑏1 ,…,𝑥i ←𝑏i]= ∑𝔼[𝑌|𝑥1 ←𝑏1 ,…,𝑥i ←𝑏i]
= ∑ i=1^m Pr[clause𝐶issatisfied|𝑥 ←𝑏 ,…,𝑥 ←𝑏]
-
The probability is
-
1 if the variables already set satisfy the clause.
-
1-(1/2)k otherwise, where k is the set of unset variables.
-
Method of conditional expectations
-
Derandomisation using conditional expectations.
-
Works for a wide variety of applications as long as
-
The variables are set independently.
-
The conditional expectations can be calculated in polynomial time.
-
Recall: Deterministic Rounding
-
For the case of vertex cover we can solve the LP-relaxation in polynomial time, to find an optimal solution.
-
The optimal solution is a “fractional” vertex cover, where variables can take values between 0 and 1.
-
We round the fractional solution to an integer solution.
-
We pick a variable xi and we set it to 1 or 0.
-
If we set everything to 0, it is not a vertex cover.
-
If we set everything to 1, we “pay” too much.
-
We set variable xi to 1 if xi ≥ 1/2 and to 0 otherwise.
-
Randomised Rounding
-
We formulate the problem as an ILP.
-
We write the LP-relaxation.
-
We solve the LP-relaxation.
-
We round the variables with probabilities that can depend on their values.
-
Let (y*, z*) be a solution to the LP-relaxation.
-
Rounding: Set xi to true independently with probability yi*.
- e.g., if y* = (1/3, 1/4, 5/6, 1/2, …) we will set variables x1, x2, x3, x4, … to true with probabilities 1/3, 1/4, 5/6, 1/2, … respectively.
MAX SAT as an ILP
Variables: yi = 1 if xi is true and 0 otherwise.
We denote clause Cj by ⋁ 𝑥𝑖 ∨ ⋁ 𝑥𝑖 𝑖∈𝑃𝑗 𝑖∈𝑁𝑗
Variables: zj = 1 if clause Cj is satisfied and 0 otherwise.
We have the inequality: ∑ 𝑦i + ∑ (1 − 𝑦i ) ≥ 𝑧j


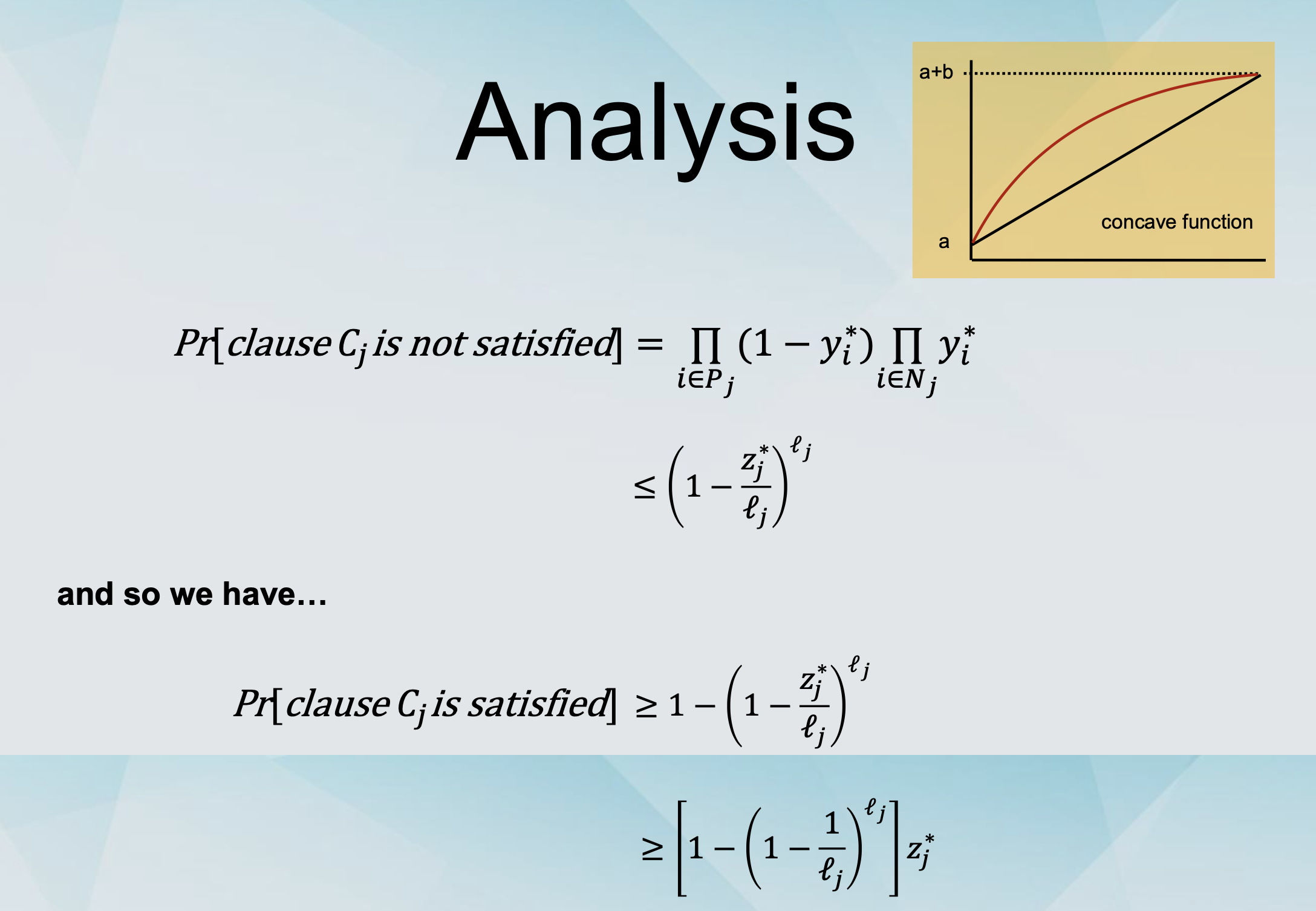

Randomised Rounding for MAX-SAT
-
Our randomised algorithm gives an approximation ratio of 1/(1-1/e) ≈ 1.59.
-
This is better than 2.
-
This is better than 1.618. (why this?)
-
Sidenote: 1.618 = φ.
The better of the two



Algorithms for MAX-SAT
-
Our Randomised Rounding algorithm gives an approximation ratio of 1/(1-1/e) ≈ 1.59.
-
This is better than 2. (unbiased coin flip for each variable)
-
This is better than 1.618. (why this?)
- Sidenote: 1.618 = φ.
-
The “better of the two” algorithm has approximation ratio 4/3 ≈ 1.33.
Back to Randomised Rounding
-
Is our RR algorithm the best possible?
-
How do we (attempt to) show that?
- Integrality gap.
Integrality Gap of MAX-SAT
-
Consider the formula: (x1 ⌵x2)⌃(┐x1 ⌵x2)⌃(x1 ⌵┐x2)⌃(┐x1 ⌵┐x2)
-
The optimal integral solution satisfied 3 clauses.
-
The optimal fractional solution sets
y1= y2 = 1/2 and zj = 1 for all j and satisfies 4 clauses.
-
The integrality gap is at least 4/3.
What does this mean?
-
We can not hope to design an LP-relaxation and rounding-based algorithm (for this ILP formulation) that outperforms our “better of the two” algorithm.
-
Can we design one that matches the 4/3 approximation ratio?
-
Yes we can!
-
Instead of “Set xi to true independently with probability yi*”,
-
We use “Set xi to true independently with probability f(yi*), for some function f.
-
Which function f?
- Any function such that 1 - 4-x ≤ f(x) ≤ 4x-1
-
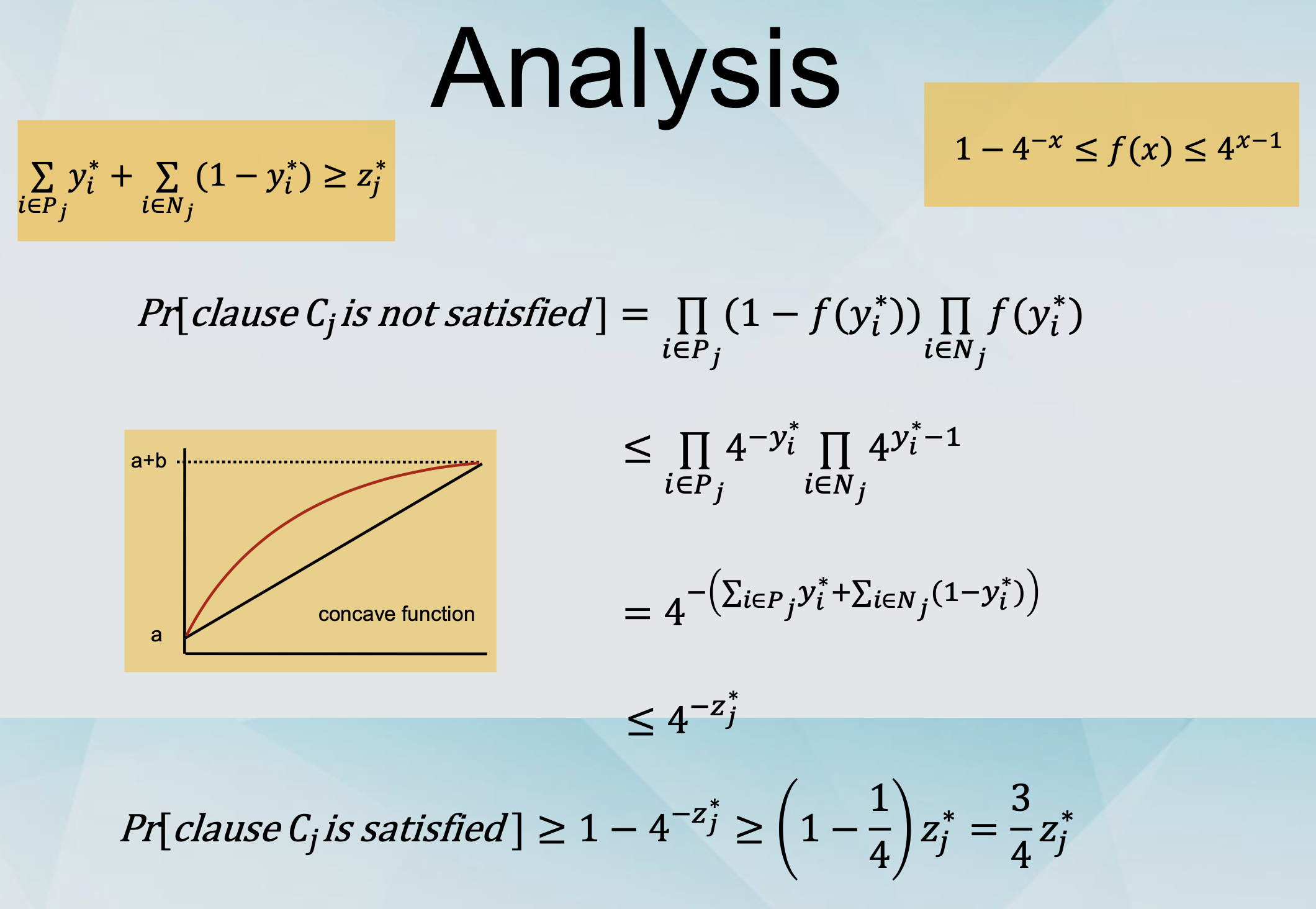

Algorithms for MAX-SAT
-
Our first RR algorithm gives an approximation ratio of 1/(1-1/e) ≈ 1.59.
-
This is better than 2. (fair coin flip for all variables)
-
This is better than 1.618. (optimal coin flip for all variables)
-
The “better of the two” algorithm has approximation ratio 4/3 ≈ 1.33.
-
The more sophisticated RR algorithm has an approximation ratio of 4/3 ≈ 1.33.