Homomorphic encryption
Encryption Enc is called homomorphic with respect to an operation * if
Enc(x \_ y) = Enc(x) _ Enc(y)That is given encrypted forms of x and y, in order to compute encrypted form of x*y one does not need to decrypt Enc(x) and Enc(y)
Partial vs Fully homomorphic schemes
-
Partially homomorphic encryption: with respect just to one operation
-
RSA (unpadded) is homomorphic with respect to multiplication
-
Fully homomorphic schemes
- With respect to multiplication and addition
- Allow to perform arbitrary computations
- Existence is by no means obvious
Potential applications
-
Computations on not entirely trusted services
- Encrypt your computational task and send it to a remote server;
- The server computes over encrypted data and returns an encrypted result;
- Decrypt result;
-
Pipeline processing without revealing intermediate data;
CryptDB
- To query encrypted SQL database without decrypting;
- Selected fields can be encrypted;
- Low overhead: reducing throughput 15-25%;
Onion-layered SQL-aware encryption
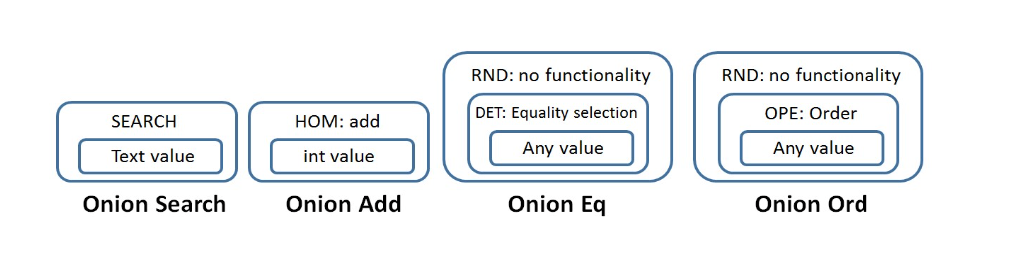
- All data in CrypDB can be encrypted using several layers of encryption;
- Each layer may “release” some information about encrypted value