Flow Networks
-
A flow network is a directed graph G=(V, E) with the following properties:
-
Each edge e in E has a nonnegative capacity ce.
-
There is a single source node s in V.
-
There is a single sink node t in V.
-
All other nodes in V - {s, t} are called internal nodes.
-
-
Further assumptions:
-
The source s does not have any incoming edges.
-
The sink t does not have any outgoing edges.
-
There is at least one edge incident to each node.
-
All the capacities are integer numbers.
-
-
Flow
-
An (s-t) flow is a function f: E → R+, mapping each edge e to a nonnegative real number f(e).
-
A (feasible) flow must satisfy the following two properties:
-
(Capacity) For each e in E, we have 0 ≤ f(e) ≤ ce
-
(Flow Conservation) For each node v in V - {s, t}, we have that

-
The Max Flow – Min Cut Theorem
-
Minimum Cut
-
A cut C is a partition of the nodes of G into two sets S and T, such that s is in S and t is in T.
-
The capacity c(S,T) of a cut C is the sum of capacities of all edges “out of S”
- these are edges (u, v) where u is in S and v is in T.
-
The Max-Flow Min-Cut Theorem
- Theorem: In every flow network, the value of the maximum flow is equal to the capacity of the minimum cut.
A series of facts
-
Fact 1: Let f by any (s-t) flow and (S, T) be any (s-t) cut. Then v(f) = fout(S) - fin(S).
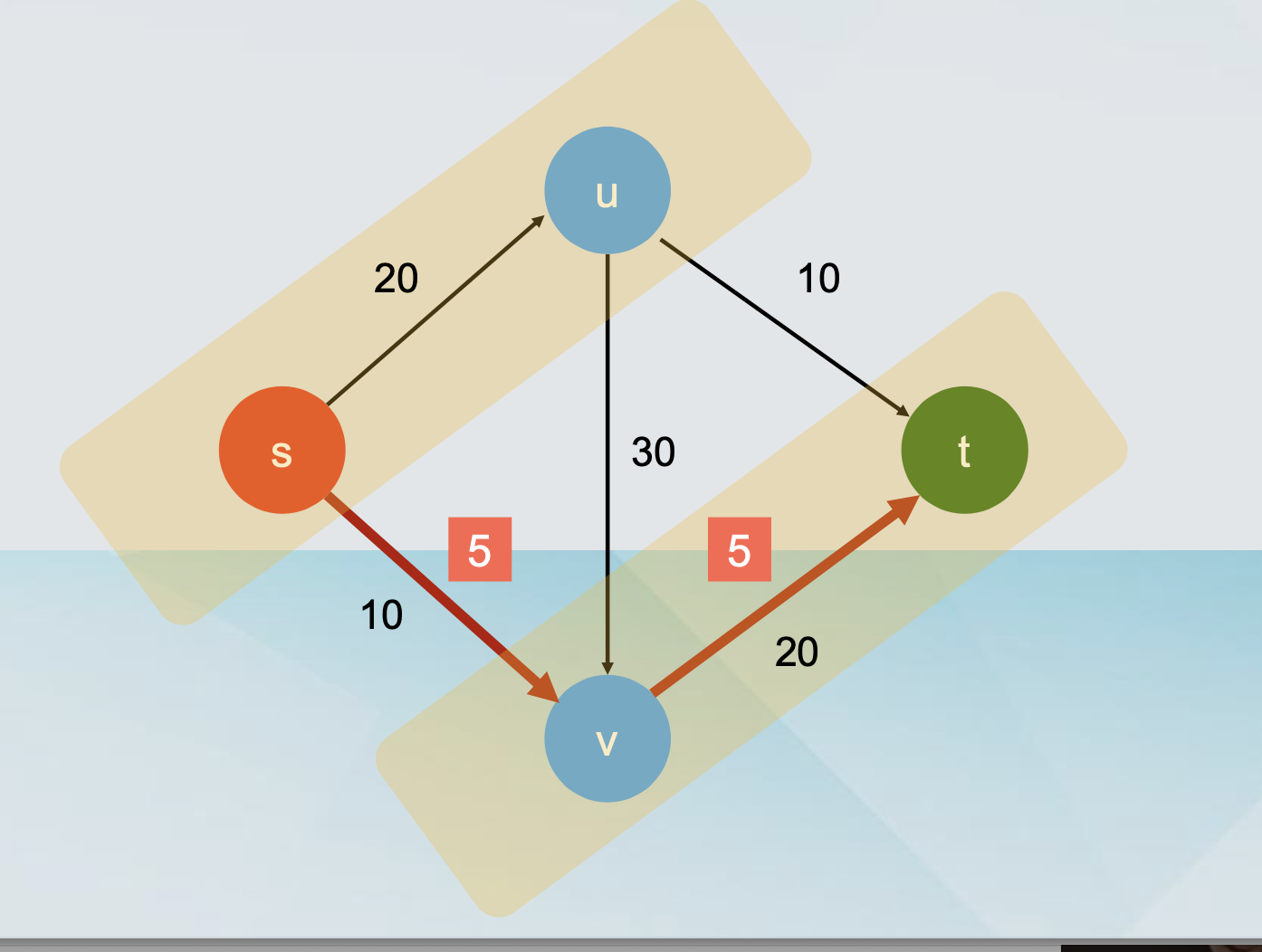
-
By definition, v(f) = fout(s).
-
By definition fin(s) = 0.
-
Hence, by definition v(f) = fout(s) - fin(s).
-
For every other node v≠s,t, we have fout(v) - fin(v) = 0
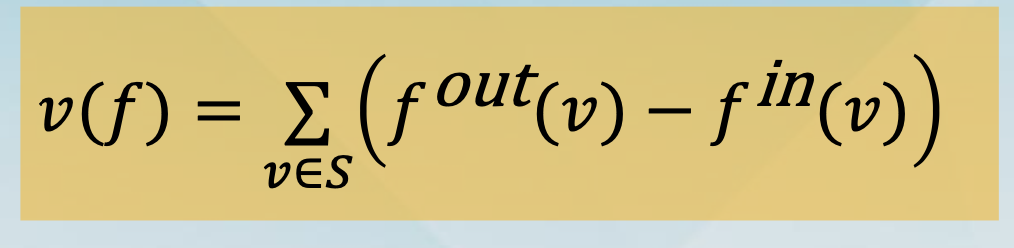
-
Let’s recount, using the edges and the flow f(e).
-
If an edge
has both endpoints in S, it is counted once for“out”and once for“in”, so it contributes 0. -
If an edge
has its “tail” in S, it is only counted for“out”and contributes 1. -
If an edge
has its “head” in S, it is only counted for“in”and contributes -1. -
Otherwise the edge does not appear in the sum.
-
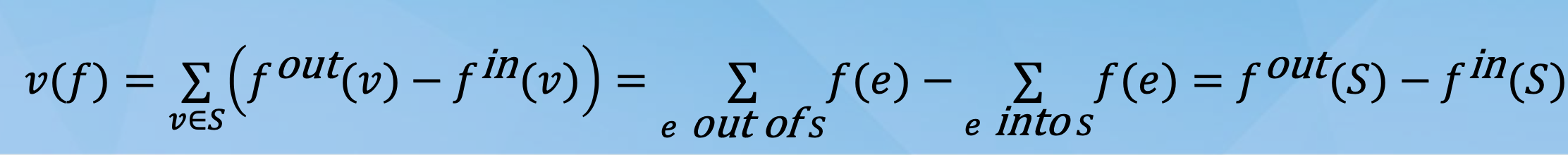
-
-
Fact 2: Let f by any (s-t) flow and (S, T) be any (s-t) cut. Then v(f) = fin(T) - fout(T).
-
Fact 3: Let f by any (s-t) flow and (S, T) be any (s-t) cut. Then v(f) ≤ c(S, T).
-
Theorem: In every flow network, the value of the maximum flow is equal to the capacity of the minimum cut.
-
Fact 4: Let f by any (s-t) flow in G such that the residual graph Gf has no augmenting paths. Then there is an (s-t) cut C(S*, T*) in G such that c(S*, T*) = v(f).
Constructing the cut
-
In the residual graph Gf, identify the nodes that are reachable from the source s.
-
Put these in S*.
-
Put the rest in T*.
-
-
Putting everything together
-
Fact 4: Let f by any (s-t) flow in G such that the residual graph Gf has no augmenting paths. Then there is an (s-t) cut C(S*, T*) in G such that c(S*, T*) = v(f).
-
Ford-Fulkerson stops when there are
no augmenting paths(无增广路径)in the residual network. -
The value of the flow is equal to the capacity of some cut.
-
This means that the value of the flow is maximum.
Integer-Valued Flows
-
Fact 5: If all the capacities in the flow network are integers, there is maximum flow for which every flow value f(e) is an integer.
-
This follows from the properties of the Ford-Fulkerson algorithm.
-
It produces a maximum flow.
-
The capacities and flows are integers in every step of the execution.
-