Profit Maximization
-
Goal: Maximize the profit.
-
Allocation Algorithm: Give the object to the player with the
highest bid. -
Payment Scheme: The winner pays an amount equal to the
second highest bid.
Bayesian Setting
-
Sometimes it makes sense to assume that some partial information is known. (部分数据已知)
-
Assume that the valuations come from a known probability distribution. The distribution is common knowledge! (估值来自一个概率分布, 这个分布是一个 knowledge)
-
Assume that you have a single player with v1∼U[0,1].
-
What sort of mechanism would we devise to maximize the expected revenue?
- We post a price p
- if v≥ p we give the item to the bidder at price p
- if v < p we keep the item
-
What is the optimal price p?

The optimal price is p=1/2 and gives us expected revenue 1/4.
Second Price Auction
-
Assume that there are two players with v1,v2∼U[0,1].
-
What is the expected revenue that we get from the second price auction?
` - Truthful auction: we consider b1(v1)=v1, b2(v2)=v2.
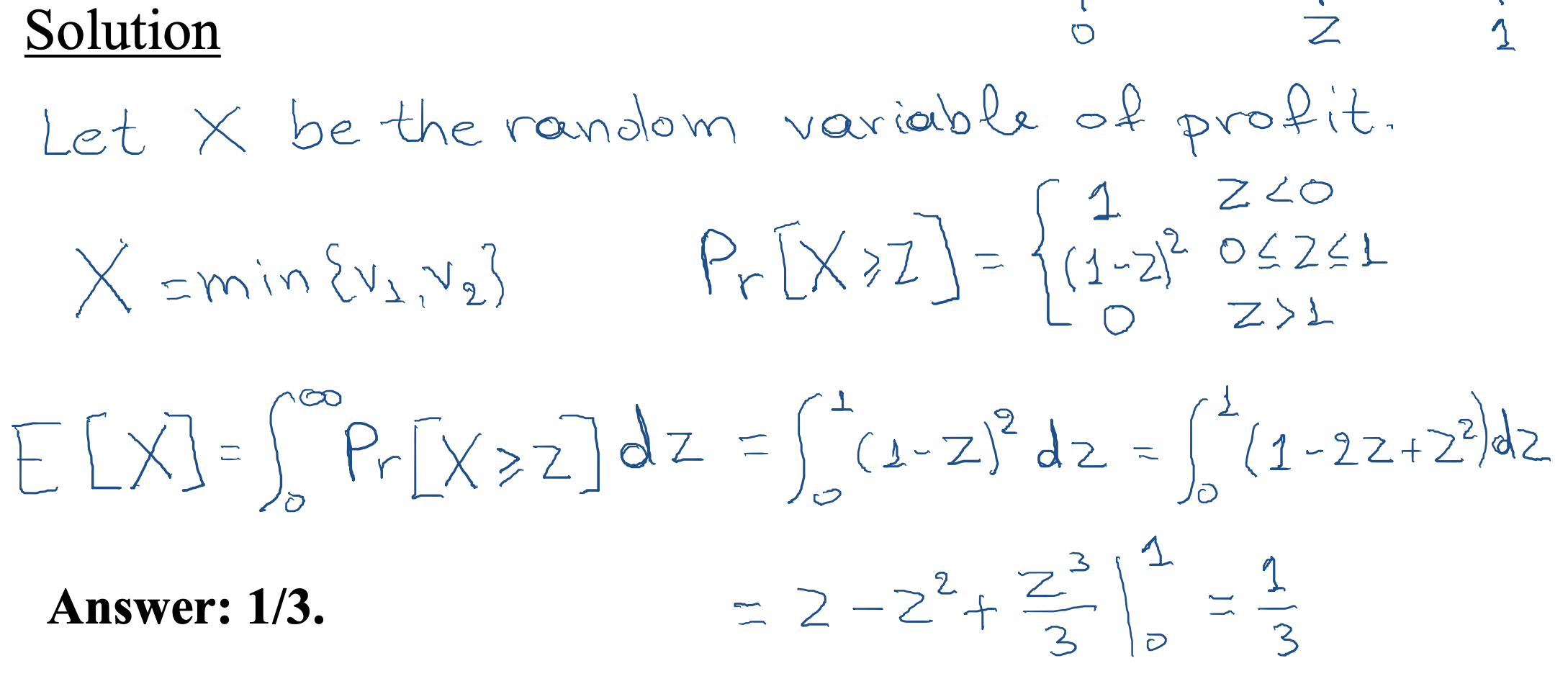
- Answer: 1/3.
First Price Auction
-
Assume that there are two players with v1,v2∼U[0,1].
-
First price auction is not truthful.
-
What is a Bayesian Nash equilibrium for the first price auction?
- Answer: b1(v1) =
v1/2, b2(v2) =v2/2. (CANVAS)
- Answer: b1(v1) =
-
Notice that the social welfare is maximized in equilibrium, i.e. we assign the item to the highest true value!
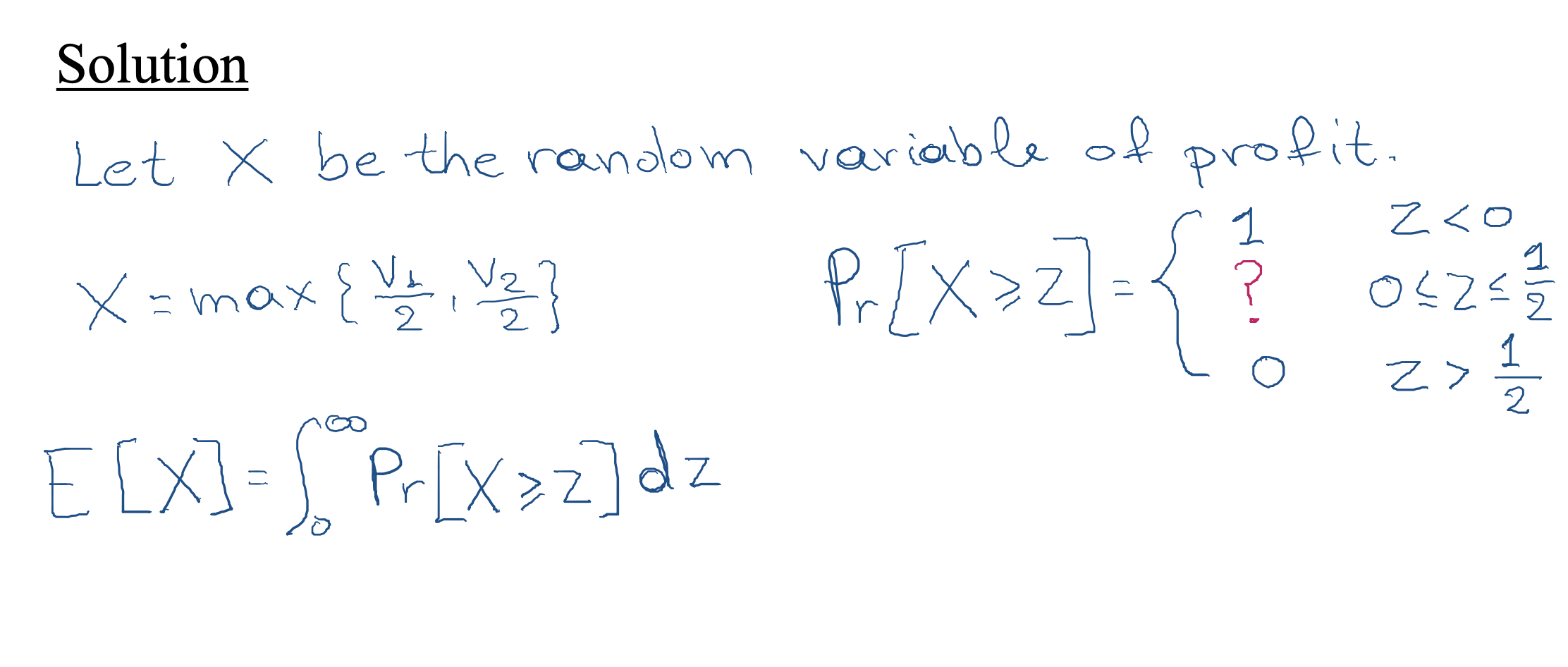
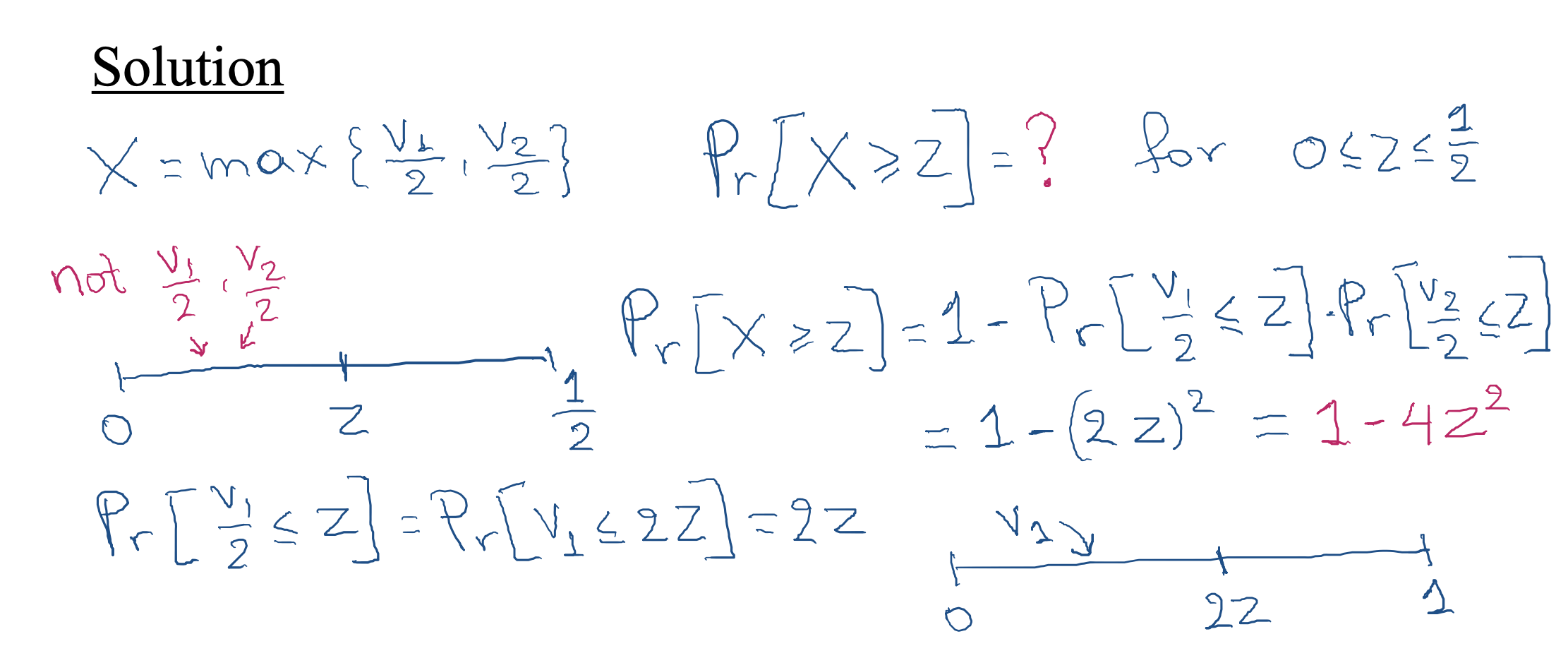

Revenue Equivalence Principle
All single-item auctions that allocate (
in equilibrium) the item to the player withhighest valueand in whichlosers pay 0, will haveidentical expected revenue.
-
Assume that there are two players with v1,v2∼U[0,1].
-
Can we improve upon the 1/3 expected revenue in a truthful way?
-
Vickrey Auction with Reserve Price 1/2.
-
if v1 < 1/2 and v2 < 1/2 we do not allocate the item
-
if v1 < 1/2 and v2 ≥ 1/2 we allocate the item to bidder 2 for price of 1/2
-
if v1 ≥ 1/2 and v2 < 1/2 we allocate the item to bidder 1 for price of 1/2
-
if v1 ≥ 1/2 and v2 ≥ 1/2 we allocate the item to the highest bidder and charge him the second highest bid.
-
-
Is this auction truthful? Yes
-
Add a dummy bidder (auctioneer) with value 1⁄2. Run Vickrey auction.
-
This auction is an affine maximizer.
-
-
What is the expected revenue that we get from this auction?
- Answer: 5/12 > 4/12 = 1/3.
-
What is the highest expected revenue that we get from this auction?

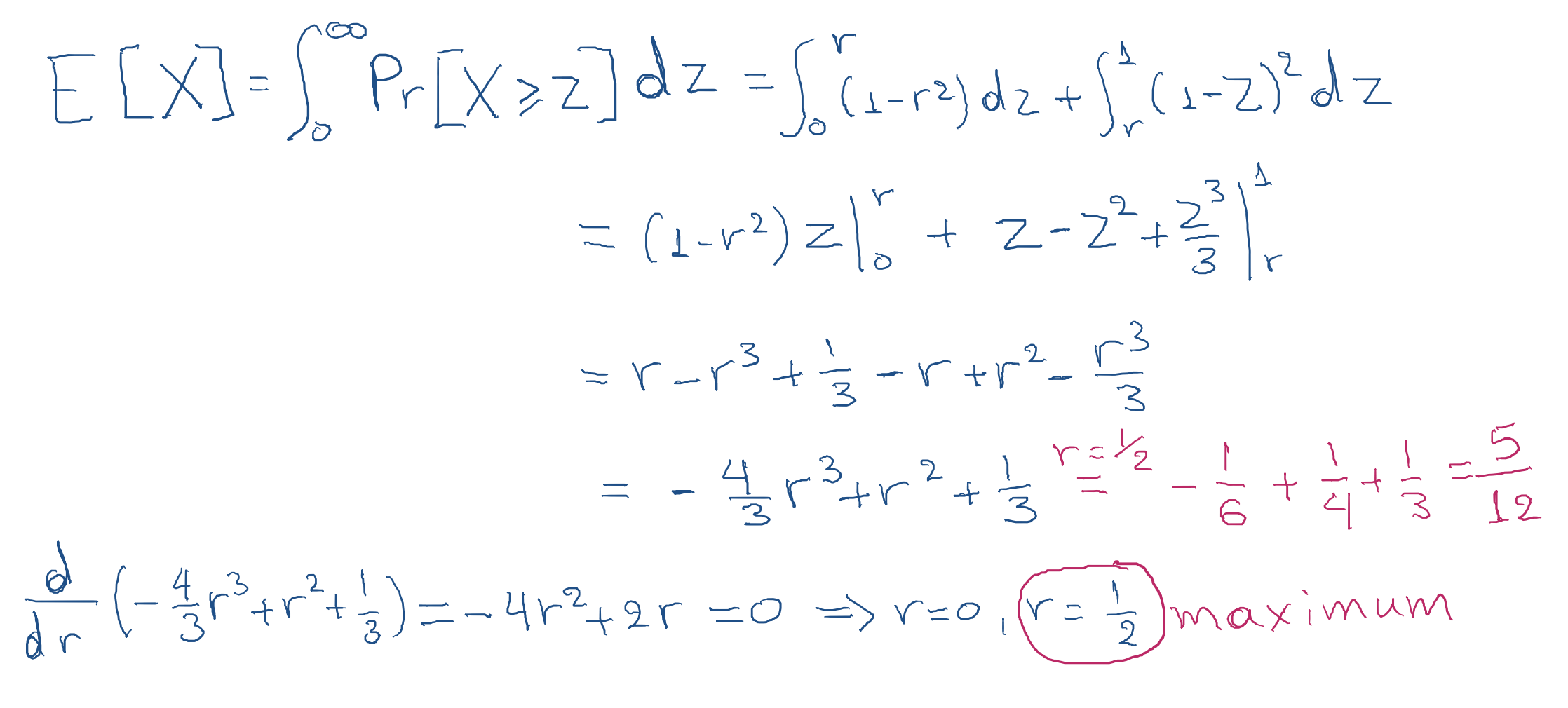
- Answer: 5/12 (r=1/2)
Single item auction
-
Definition
-
Assume that there are n bidders with vi ∈ [0,h].
-
Mechanism M(x, p1, … , pn)
-
Input: b=(b1,…,bn) the vector of declarations
-
Output: x(b) allocation function
-
xi(b)=1 if i gets the item
-
xi(b)=0 if i does not get the item
-
-
Output: p1(b),…,pn(b): payment functions
-
The utility of player i if his true value is vi but he reports bi is
ui(bi,b-i;vi)= vi⋅xi(bi,b-i)-pi(bi,b-i)
-
-
Notice that player i’s valuation is a single-parameter.
-
A mechanism is truthful if for every i, bi,vi,b-i
ui(vi,b-i;vi) ≥ ui(bi,b-i;vi)
vi⋅xi(vi,b-i)-pi(vi,b-i) ≥ vi⋅xi(bi,b-i)-pi(bi,b-i)
-
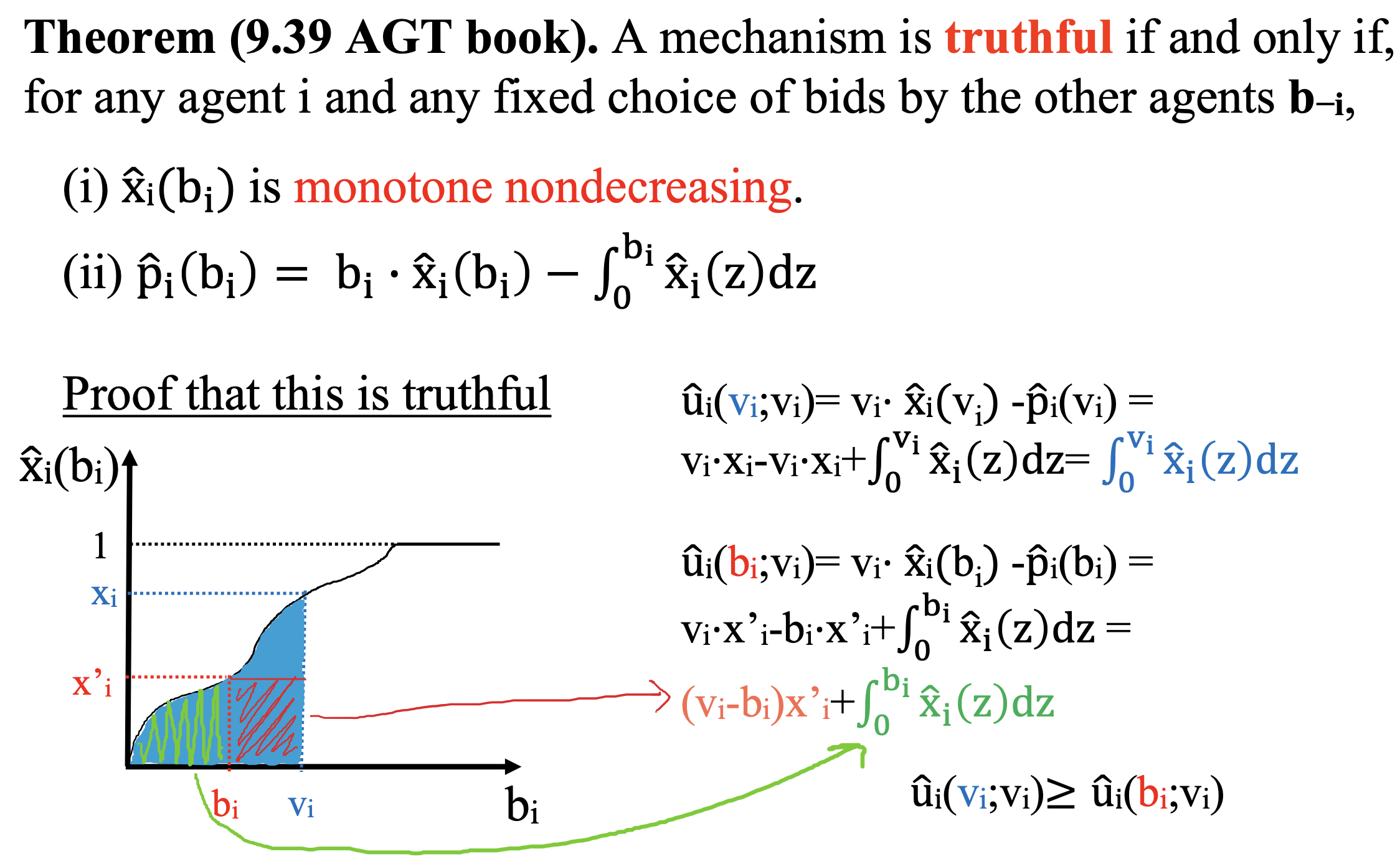
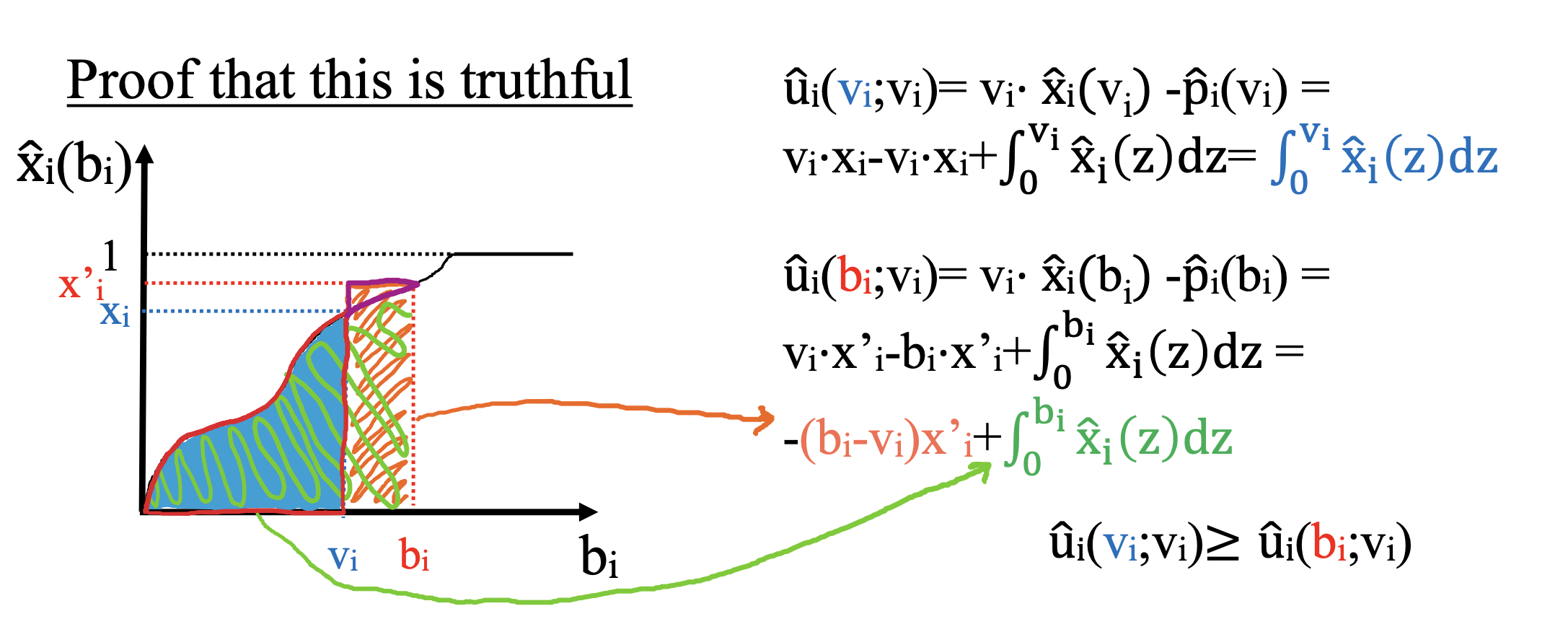
Theorem (9.39 AGT book). A mechanism is truthful if and only if, for any agent i and any fixed choice of bids by the other agents b−i,

-
Example:

Virtual valuations
-
Definition. The virtual valuation of agent i with valuation vi is
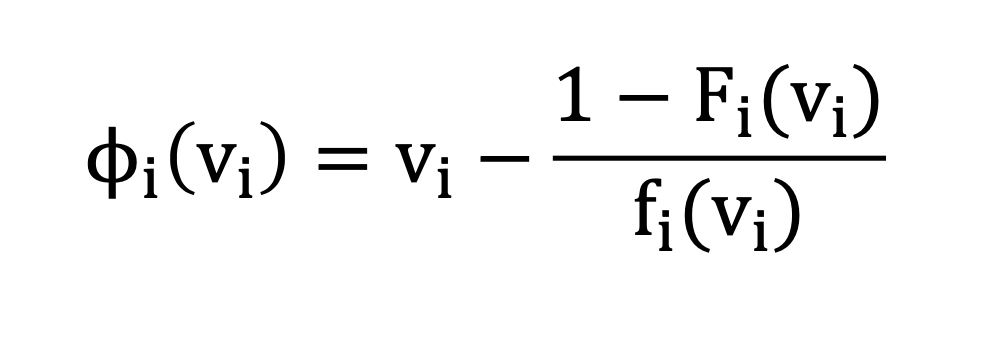
-
Definition. Given valuations, vi , and corresponding virtual valuations, φi(vi), the virtual surplus (social welfare) of allocation x is
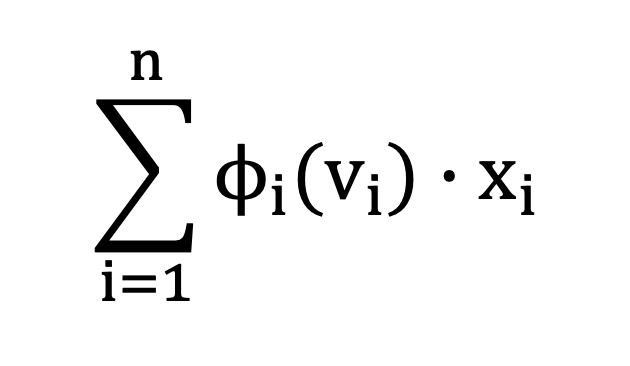
-
Theorem. The expected profit of any truthful mechanism, M, is equal to its expected virtual surplus
- example
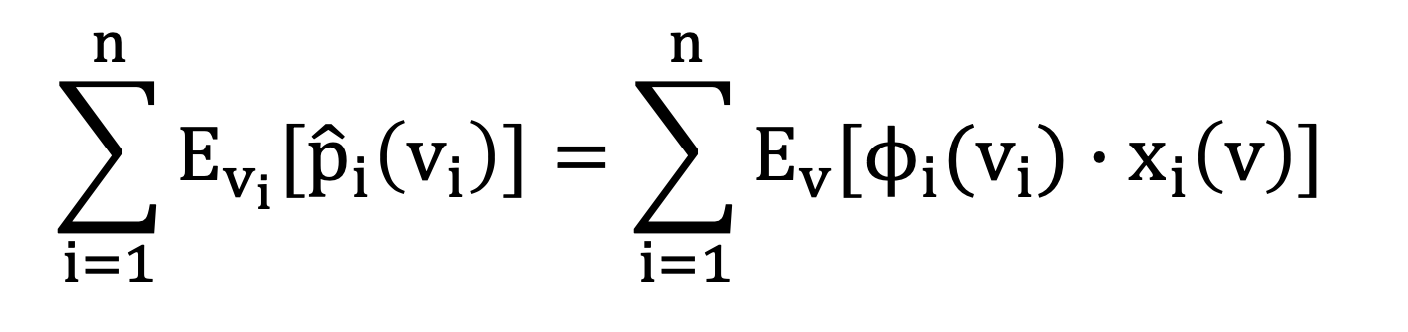
-
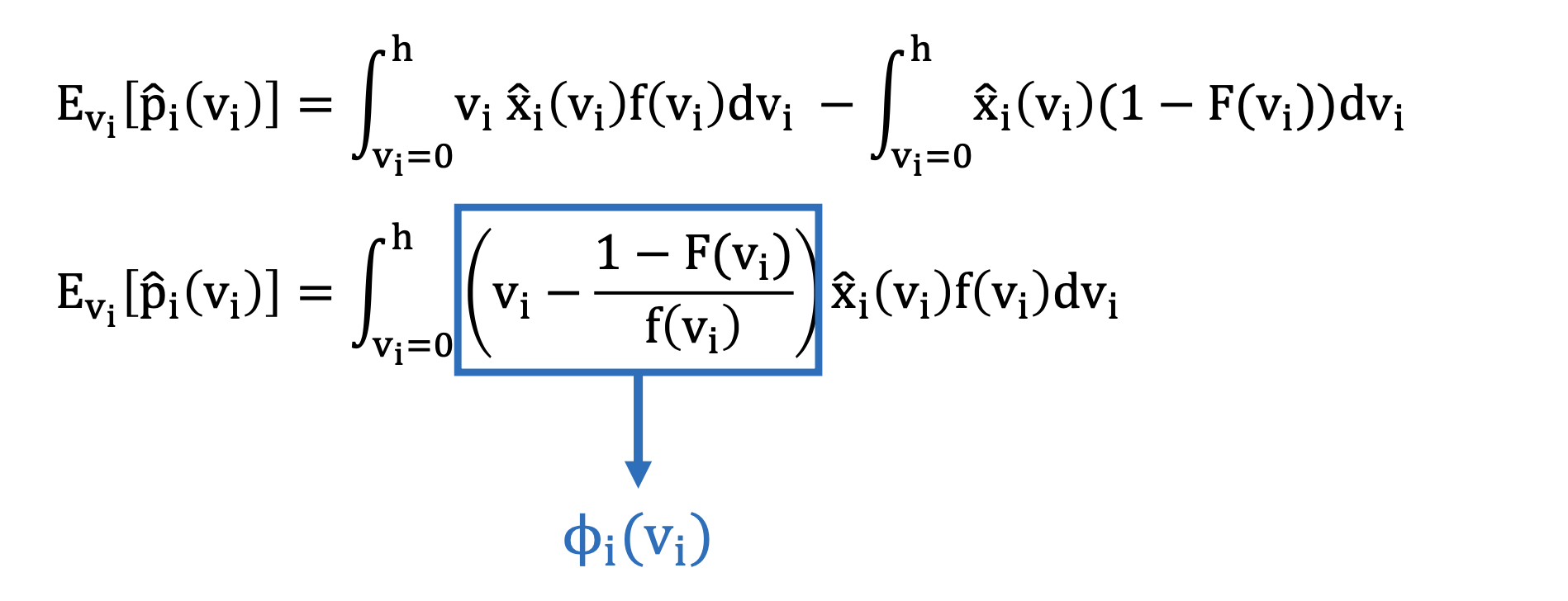
Lemma. Consider any truthful mechanism and fix the bids v−i of all bidders except for bidder i. The expected payment of a bidder i satisfies:
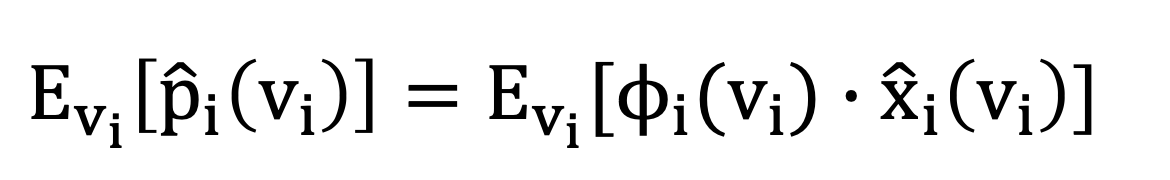
-
proof:

-
-
Lemma. Virtual surplus maximization is truthful if and only if, for all i, φi(vi) is monotone nondecreasing in vi.
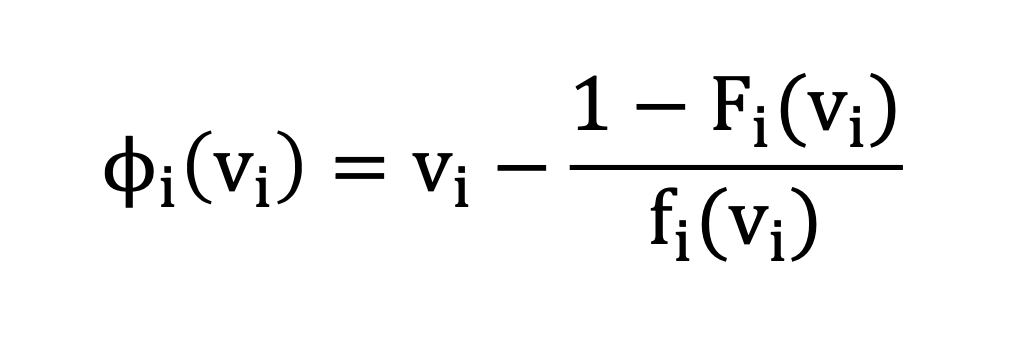
Myerson’s Optimal Mechanism
-
Definition: MyeF(b)
-
Given the bids b and F, compute “virtual bids”: b′i = φi(bi).
-
Run VCG on the virtual bids b′ to get x′ and p′
-
Output x = x′ and p with pi = φ−1i (p′i) (upon winning).
-



-
MyeF(v1,v2): Vickrey Auction with Reserve Price 1/2
-
Q: Can we do better?
- No, Mayerson’s mechanism is optimal.