Load Balance Games
-
Makespan scheduling on uniformly related machines
-
n tasks with weights w1,…,wn
-
m parallel mach in es with speeds s1,…,sm
- identical machines: s1 = s2 = ··· = sm = 1 I uniformly related machines: else
- A:[n]7→[m]…assignmentoftaskstomachines
-
The load of machine j∈[m] under the assignment A is:

-
Objective: minimize the make span, aka the maximum load overall machines
Definition of Load balancing games
- The task i∈[n] is managed by player
i - The pure strategy A(i) for each player i∈[n] yields an assignment A : [n] 7→ [m]
- Given an assignment
A- the cost of player i is the load of the chosen machine l_A(i)
- the social cost is the makespan: cost(A) = maxj∈[m]{l_j}
Pure Nash equilibrium
An assignment A is a pure Nash equilibrium if for all players i ∈ [n] and all machines j ∈ [m]:
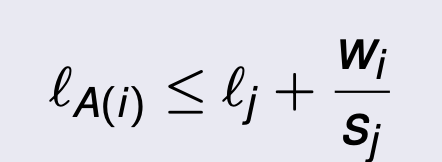
largest Processing Time (LPT)
- The Largest Processing Time (LPT) scheduling algorithm computes a pure Nash equilibrium in polynomial time. // 计算纯纳什均衡多项式时间
Algorithm
-
Start with empty assignment: lj := 0 for all j ∈ [m]
-
Sort task in non-increasing order w1 ≥ w2 ≥ ··· ≥ wn
-
For i from 1 to n do
- A(i) := arg minj∈[m]{lj + wi }
- lA(i):=lA(i)+wi
-
returnA
function LPTAlgorithm(arr) {
var res = [];
arr.forEach((val) => {});
}
Corollary 2.2
Every instance of the load balancing game admits a pure Nash equilibrium. // 所有负载平衡游戏的实例都可以使用纯纳什均衡
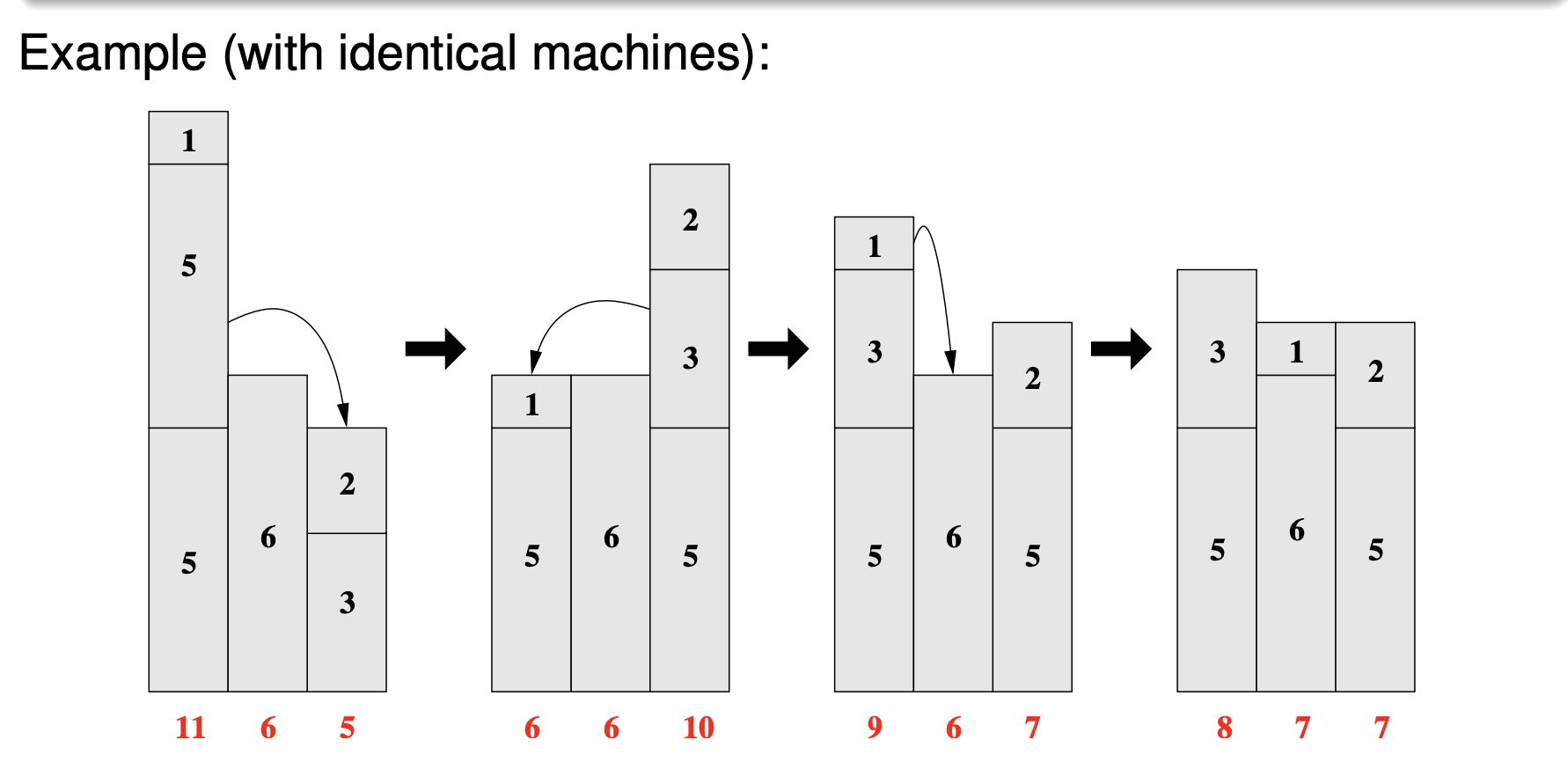
Best response sequences 1
-
Improvement step: change to best response
-
Single player moves his task to the machine that minimizes his cost. // 减少花销
-
Example:
-
Best response sequences 2
-
Best response sequences
-
take the strategic nature of the players into account
-
model convergence
-
-
Theorem 2.3
For every instance of the load balancing game with
related machinesevery best response sequence terminates. -
Remark
- There are instances with identical machine that have sequences of length Ω(2^√n).
Best response sequences 3
-
Theorem 2.4
- For identical machines the length of any sequence of best responses is at most 2^n. // 对于相同的机器,任何最佳响应序列的长度都不超过 2^n
-
Theorem 2.5
- Let A : [n] → [m] denote any assignment of n tasks to m identical machines. Starting from A, the max-weight best response policy reaches a pure Nash equilibrium after each agent was activated at most once.
-
Lemma 2.6
- Suppose task i makes a best response: For all tasks j with wj ≥ wi , if j was satisfied before, it remains satisfied after i’s best response.
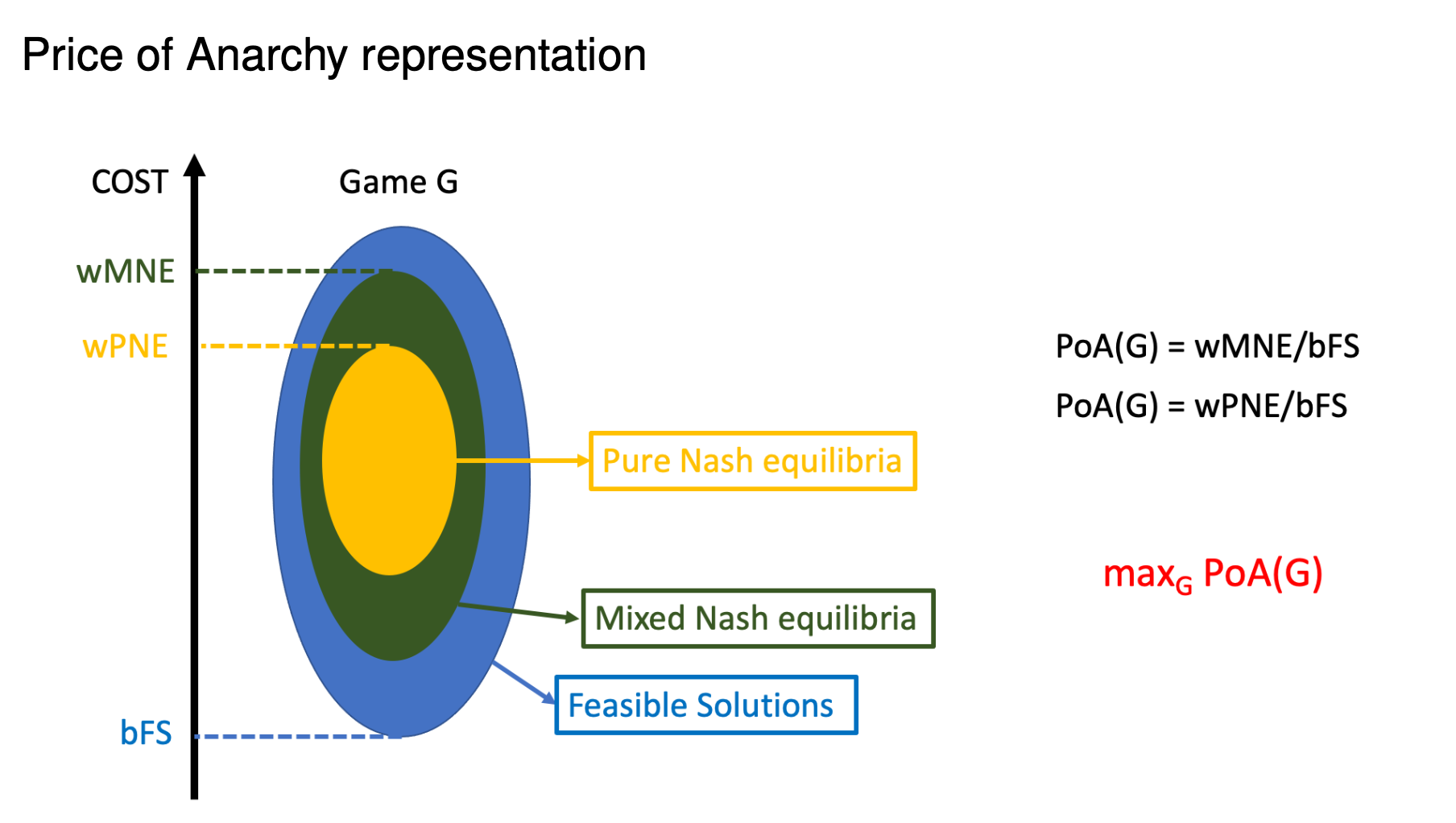
Price of Anarchy: Definition
- Price of anarchy: The
worst case ratiobetween the social cost in some Nash equilibrium (NE) and the optimum social cost.

-
Goal: Find the exact PoA for a class of games and type of equilibria.
-
Upper bound α: show that for all such instances and all such equilibria the PoA is at most α.
-
Lower bound α: find such an instance and such an equilibrium where the PoA is at least α.
Bounds on the Price of Anarchy

-
Form=2,theexampleonpreviousslideprovesthelowerbound in blue.
-
Exercise:
Generalise this example to match the bound for all m.