Gradient Descent
- Gradient Descent is an algorithm that can use to try to minimize any function.
Gradient Descent outline
- Start with some w,b (attributes)
- Keep changing w,b to reduce J(w, b)
- Until we settle at or near a minimum
Gradient Descent algorithm
$$ w = w - \alpha \frac{\partial{}}{\partial{w}}J(w, b) $$
$$ b = b - \alpha \frac{\partial{}}{\partial{b}}J(w, b) $$
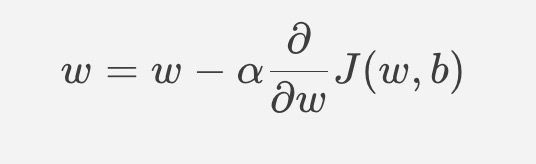
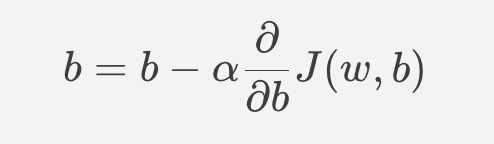
- \alpha means the learning rate, which is between 0 to 1.
- Derivative term
- Correct: Simultaneously update w and b
The principle of Gradient Descent algorithm

How to choose Alpha (Learning rate)
- If the learning rate is too small then gradient descent will work, but it will be slow.
- By contrast, if the learning rate is too large then gradient descent may overshoot and never reach minimum.
Running gradient descent
“Batch” Gradient descent
- Batch: Each step of gredient descent uses all of the training examples