Public-key, or asymmetric encryption

• Public-key encryption techniques. It is particular and most important kind of
• Asymmetric encryption (or asymmetric key encryption):
  • One key is used for encryption (usually publicly known, public key);
  • Another key is used for decryption (usually private, or secret key)

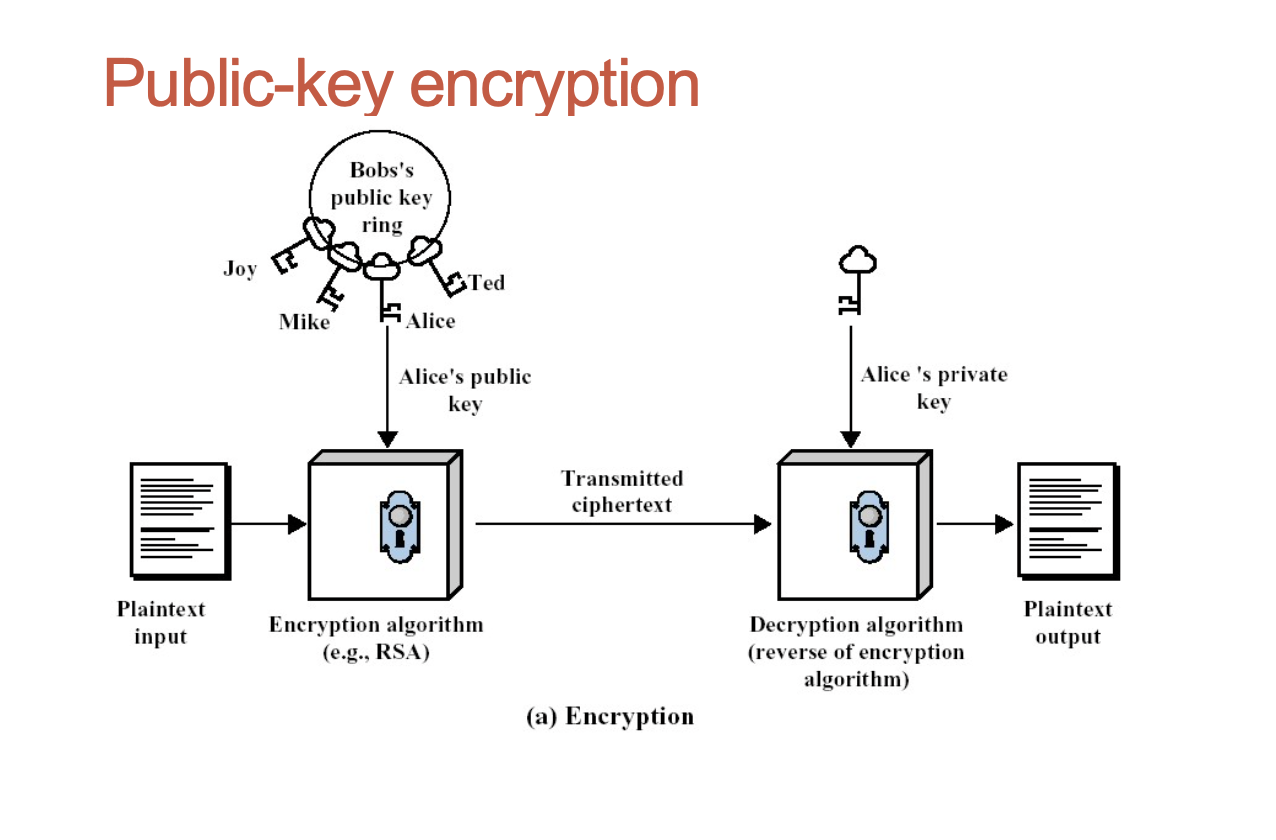
Essential steps in communications using public-key encryption

• Each user generates a pair of keys;
• Each users makes one of the key publicly accessible (public key). The other key of the pair is kept private;
• If B wishes to send a private message to A, B encrypts the message using A’s public key;
• When A receives the message, A decrypts it using A’s private key. No other recipient can decrypt the message
  • nobody else knows A’s private key.

Public-key encryption

• Advantages

  • All keys (public and private) are generated locally;
  • No need in distribution of the keys;
  • Moreover, each user can change his own pair of public/private key at any time;

• Disadvantages

  • It is more computationally expensive.

Public-Key Cryptosystems

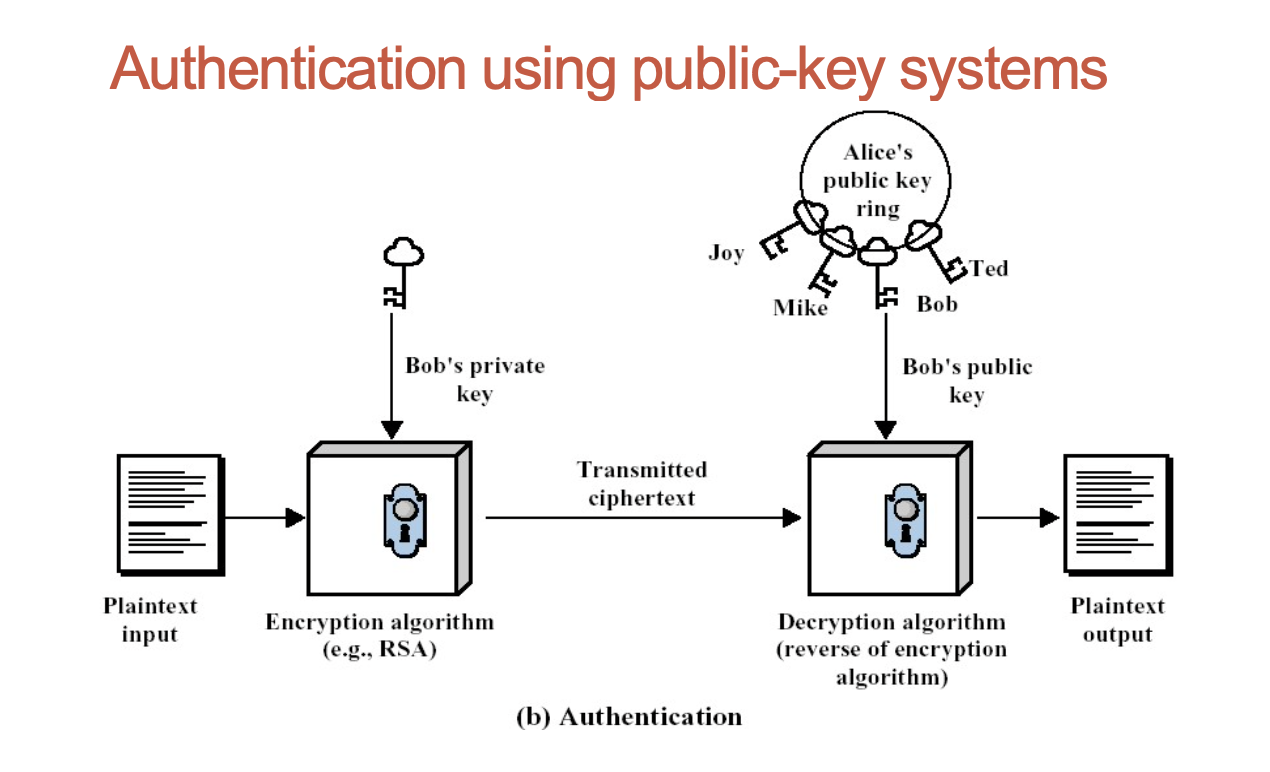
• Encryption/decryption: the sender encrypts a message with the recipient’s public key.
• Digital signature (authentication): the sender “signs” the message with its private key; a receiver can verify the identity of the sender using sender’s public key.
• Key exchange: both sender and receiver cooperate to exchange a (session) key.

• Diffie and Hellman conditions
  • “Easy part”
    • It is computationally easy for a party B to generate a pair (public key , private key).
    • It is computationally easy for a sender A, knowing the public key of B and the message M to generate a ciphertext:
    • It is computationally easy for the receiver B to decrypt the resulting ciphertext using his private key
  • Difficult part
    • It is computationally infeasible for anyone, knowing the public key, to determine the private key
  • Additional useful requirement (not always necessary)
    • Either of the two related keys can be used for encryption, with the other used for decryption.

Public-key cryptography and number theory

• Many public-key cryptosystems use non-trivial number theory(非平凡数论？？？);

• Security of most known RSA public-key cryptosystem is based on the hardness of factoring big numbers (基于分解大数的难度);

• We will overview basic notions of divisors, prime numbers, modular arithmetic

Divisors and prime numbers

• Divisors
  • Let a and b are integers and b is not equal to 0;
  • thenwesaybisadivisorofaif thereisanintegerm such that a = mb;
• Prime numbers(质数)
  • An integer p is a prime number if its only divisors are 1, - 1, p, -p

gcd(最大公约数) and relatively prime numbers

• gcd(a,b) is a greatest common divisor of a and b
  • Examples: gcd(12, 15) = 3; gcd(49,14) = 7.
• a and b are relatively prime if gcd(a,b) = 1.
  • Example: gcd (9,14) = 1.

Modular arithmetic（模运算）

• If a is an integer and n is a positive integer, we define a mod n to be the remainder when a is divided by n:
  • a = qn+r,
    • Hereqisaquotient andr=amodn
• If (amodn) = (bmodn)then a and b are congruent modulo n;
• It is easy to see,that (amodn) = (bmodn) iff n is a divisor of a-b.

Modular arithmetic. Properties

• [(amodn)+(bmodn)] mod n = (a+b) mod n
• [(amodn)–(bmodn)] mod n = (a-b) mod n
• [(amodn) x (bmodn)] mod n= (axb) mod n
• Example: 3 mod 5 x 4 mod 5 = 12 mod 5 = 2 mod 5

RSA algorithm

• One of the first, and probably best known public-key scheme;
• It was developed in 1977 by R.Rivest, A.Shamir and L. Adleman;
• RSA is a block cipher in which the plaintext and ciphertext are integers between 0 and n-1, where n is some number;
• Every integer can be represented, of course, as a sequence of bits;

Private and Public keys in RSA

• Public key KU = {e,n};

• Private key KR = {d,n};

• Requirements:

  • It is possible to find values e,d,n such that
  • It is easy to calculate

• It is possible to find values e,d,n such that

• (key generation) , where k is some number , k < n

• It is easy to calculate and modulo n • It is difficult to determine d given e and n

Key generation

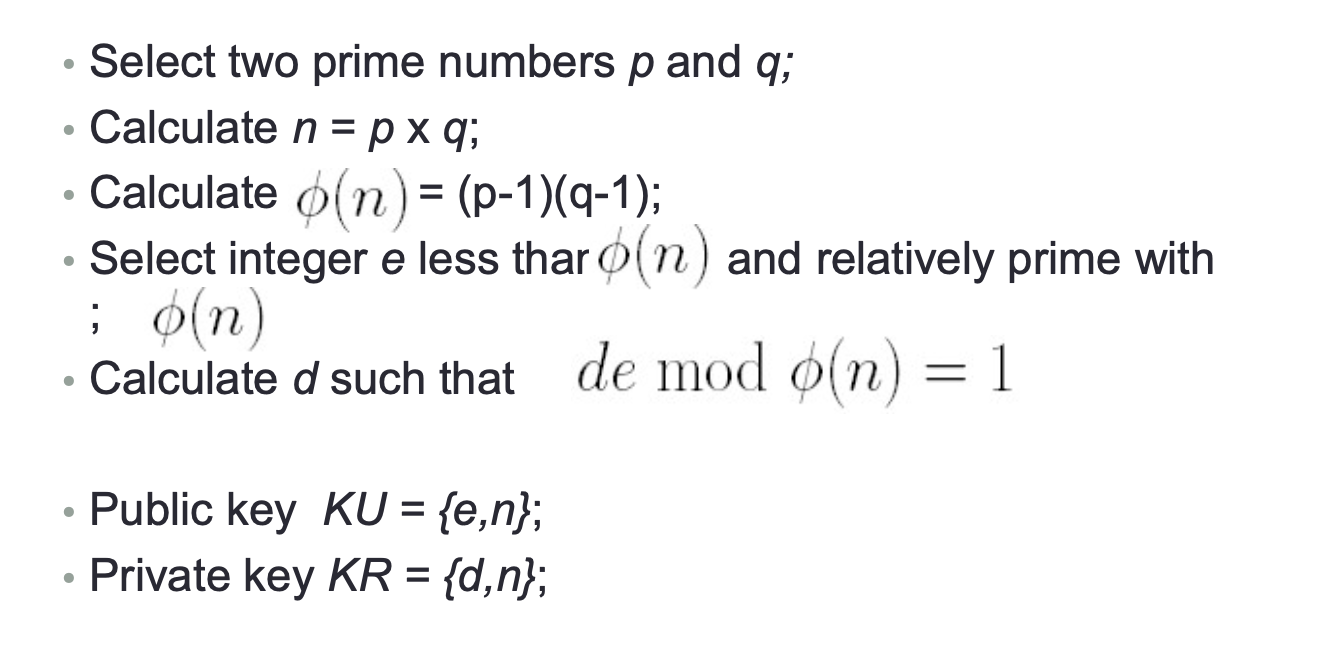
Fermat – Euler Theorem

Chinese Remainder Theorem

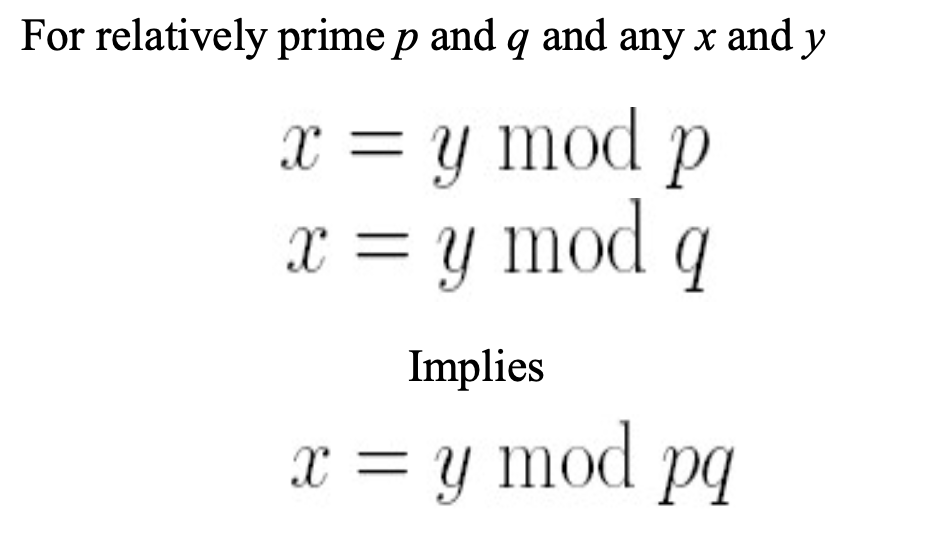
• Select two prime numbers, p = 17, q = 11;
• Calculate n = pq = 187;
• Calculate = 16 x 10 = 160;
• Select e less than 160 and relatively prime with 160;
• Lete=7;
• Determinedsuchthat demod160=1andd<160.The correct value is d = 23, indeed 23 x 7 = 161 = 1 mod 160.
• Thus KU = {7,187} and KR = {23,187} in that case.

Security of RSA

• Relies upon complexity of factoring problem:
• Nobody knows how to factor the big numbers in the reasonable time (say, in the time polynomial in the size of (binary representation of ) the number (unless you go to quantum computing!) ;
• On the other hand nobody has shown that the fast factoring is impossible;