Graph Definitions

• Graph G=(V,E)

• Set of vertices (or nodes) V, with |V| = n Set of edges E, with |E| = m

• Undirected: edge e = {v,w} (or just vw) Directed: edge e = (v,w)

• Neighbours of a vertex v : Set of nodes connected by an edge with v Degree of a vertex v : number of neighbours of v, denoted deg(v)

• Directed graphs: in-degree and out-degree

• Path: A sequence of (non-repeating) nodes with consecutive nodes being connected by an edge.

  • Length: # nodes – 1 = # edges

• Distance between u and v : length of the shortest path u and v

• Graph diameter: The longest distance in the graph

Adjacency Matrix （邻接矩阵）

• The ith node corresponds to the ith row and the ith column.
• If there is an edge between i and j in the graph, then we have A[i,j] = 1, otherwise A[i,j] = 0.
• For undirected graphs, necessarily A[i,j] = A[j,i]. For directed graphs, it could be that A[i,j] ≠ A[j,i].

Adjacency List （邻接链表）

• Nodes are arranged as a list, each node points to the neighbours.

• For undirected graphs, the node points only in one direction.

• For directed graphs, the node points in two directions, for in- degree and for out-degree

	Adjacency Matrix	Adjacency List
Memory	O(n^2)	O(m+n)
Checking adjacency of u and v Time	O(1)	O(min(deg(u),deg(b)))
Finding all adjacent nodes of u Time	O(n)	O(deg(u))

Depth-First Search （深度优先搜索）

Definition

• A connected component of a graph G is subgraph such that any two vertices are connected via some path.

Description in words

• We wander through a labyrinth with a string and a can of red paint.

• We start at a node s and we tie the end of our string to s. We paint node s as visited.

• We will let u denote our current vertex. We initialise u = s

• We travel along an arbitrary edge (u,v).

• If the (u,v) leads to a visited vertex, we return to u. • Otherwise, we paint v as visited, and we set u = v • Then, we return to the beginning of the step.

• Once we get to a dead end (all neighbours have been visited), we backtrack to the previously visited vertex p. We set u = p and repeat the previous steps.

• When we backtrack back to s, we terminate the process.

Visualising Depth-First Search

• Orient the edges along the direction in which they are visited during the traversal.

  • Some edges are discovery edges, because they lead to unvisited vertices.

  • Some edges are back edges, because they lead to visited vertices.

• The discovery edges form a spanning tree of the connected component of the starting vertex s.

Example

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
var hasPathSum = function (root, targetSum) {
  if (!root) return false;
  let res = false;
  const dfs = (n, s) => {
    if (!n.left && !n.right && s === targetSum) {
      res = true;
    }
    if (n.left) dfs(n.left, s + n.left.val);
    if (n.right) dfs(n.right, s + n.right.val);
  };
  dfs(root, root.val);
  return res;
};

Breadth-First Search 广度优先

• Simple description

  • Start from the starting vertex s which is at level 0 and consider it explored.

  • For any node at level i, put all of its unexplored neighbours in level i+1 and consider them explored.

  • Terminate at level j, when none of the nodes of the level has any neighbours which are unexplored.

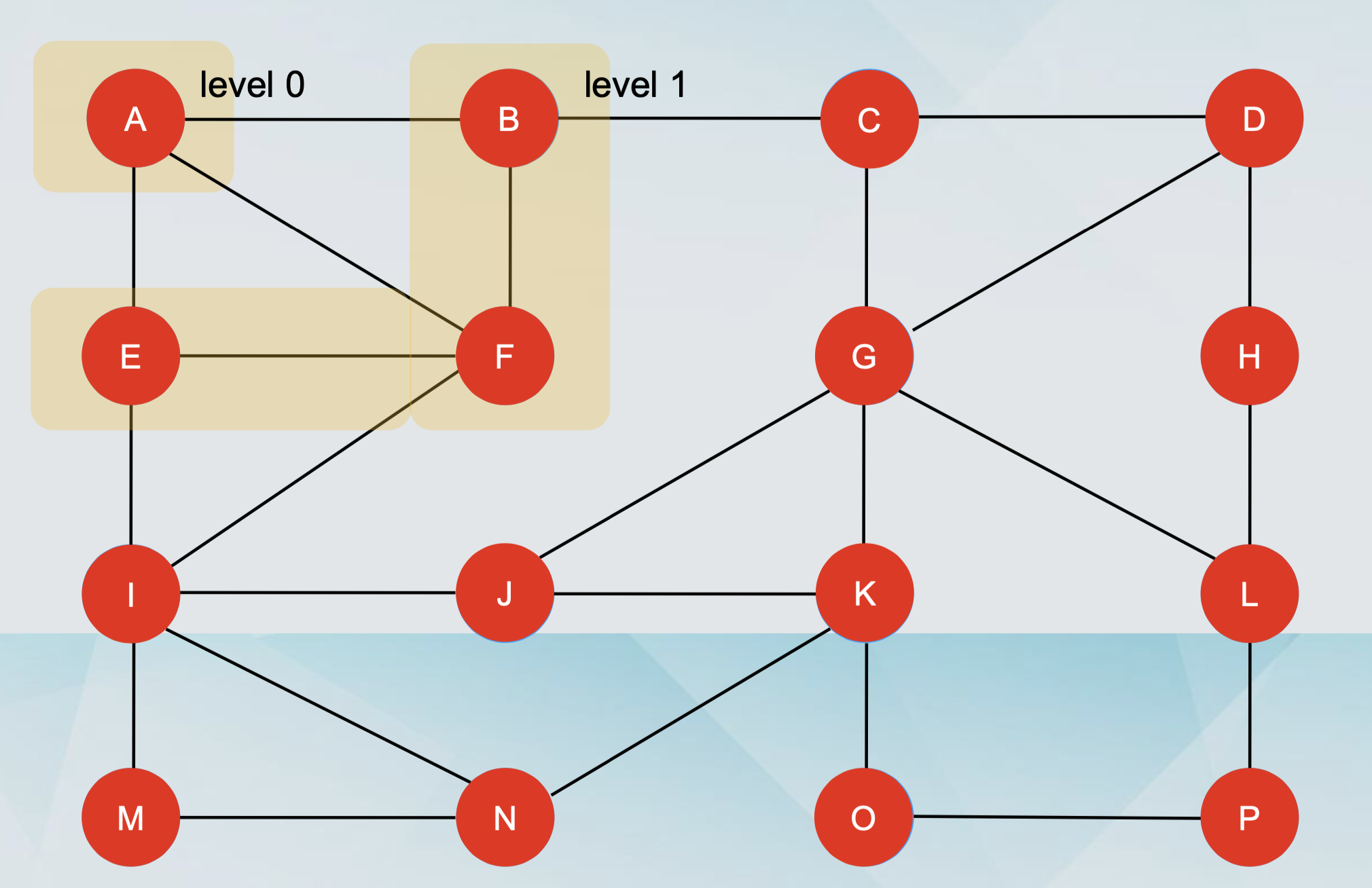
Visualising Breadth-First Search

• Orient the edges along the direction in which they are visited during the traversal.

  • Some edges are discovery edges, because they lead to unvisited vertices.

  • Some edges are cross edges, because they lead to visited vertices.

• The discovery edges form a spanning tree of the connected component of the starting vertex s.

Properties of BFS

• For simplicity, assume that the graph is connected.

• The traversal visits all vertices of the graph.

• The discovery edges form a spanning tree.

• The path of the spanning tree from s to a node v at level i has i edges, and this is the shortest path.

• If e=(u,v) is a cross edge, then the u and v differ by at most one level.

Running time of BFS

• O(m + n)

Testing for bipartiteness

Bipartite graphs （二分图）

• A graph G=(V,E) is bipartite if any only if it can be partitioned into sets A and B such that each edge has one endpoint in A and one endpoint in B. // 一个图仅仅可以被划分为 A，B 两个 set，且每个 set 有一个 endpoint

• Often, we write G=(A U(union) B,E).

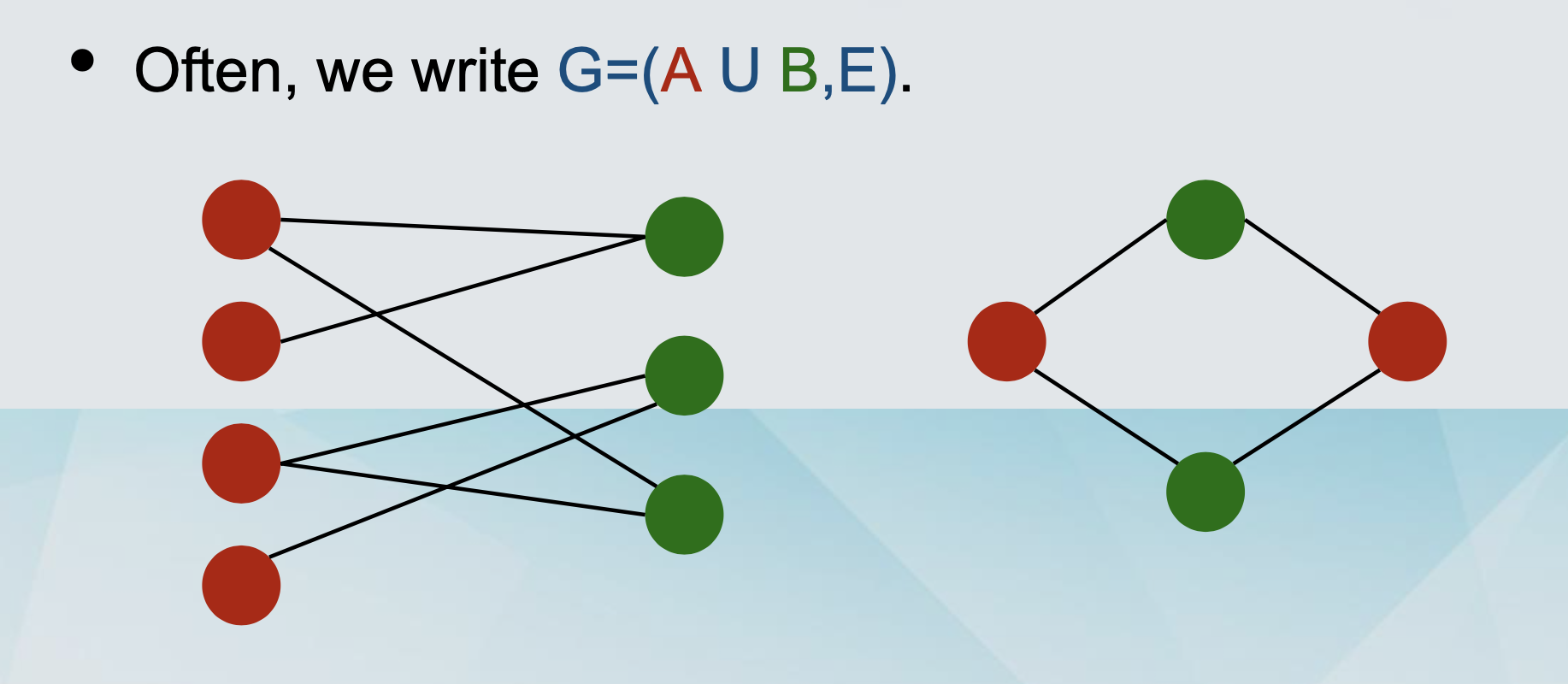
• Alternative definitions

  • A graph G=(V,E) is bipartite if any only if its nodes can be coloured with 2 colours (say red and green), such that every vertex has one red endpoint and one green endpoint.

  • A graph G=(V,E) is bipartite if any only if it does not contain any cycles of odd length.

No odd cycles 无奇数环

• A graph G=(V,E) is bipartite if any only if it does not contain any cycles of odd length.

• => Assume that G is bipartite

• Suppose that G does contain an odd cycle (proof by contradiction), C = u1 u2 u3 … un u for some u in A (wlog), or alternatively, for some u that is red.

• Because G is bipartite, u2 must be green, and then u3 must be red, and so on.

• Generally, we observe that for all k in {1,2, … ,n}, uk is red if k is odd and green if k is even.

• By assumption, n is odd, so it must be red. But then u cannot be red, because G is bipartite.

• Alternative definitions

• A graph G=(V,E) is bipartite if any only if its nodes can be coloured with 2 colours (say red and green), such that every vertex has one red endpoint and one green endpoint.

• A graph G=(V,E) is bipartite if any only if it does not contain any cycles of odd length.

• Sometimes, these alternatives definitions are also called “characterisations”.

Testing bipartiteness

• Given a graph G=(V,E), decide if it is bipartite or not.

• Given a graph G=(V,E) decide if it is 2-colourable or not.

• Given a graph G=(V,E) decide if it is contains cycles of odd length or not.

Colouring the nodes

• Does this remind you of something?

  • It is essentially BFS!

  • We label the nodes of level 1 red, the nodes of level 2 green, and so on.

• Implementation:

  • Add a check for odd/even and assign a colour accordingly.

  • In the end, check all edges to see if they have endpoints of the same colour.

Correctness

• Suppose that G is bipartite. Then, all cycles must be of even length.

• Suppose to the contrary that the algorithm returns “not bipartite”.

  • This means that it has found an edge e=(x,y) with endpoints of the same colour.

  • Since the endpoints of any edge can not differ by more than one layer and layers have alternating colours, x and y must be in the same layer.

Strong Connectivity (强连通性)

Directed graphs

• Nodes are arranged as a list, each node points to the neighbours.

• For directed graphs, the node points in two directions, for in-degree and for out-degree.

• DFS and BFS on directed graphs

  1. Very similar to their version on undirected graphs.
  2. When we are at a node and we examine its neighbours, a neighbour is now only a node that we can reach with a directed edge.
  3. The running time is still O(n+m).

Connectivity

• What BFS is computing is the set of nodes t such that there is a path from s to t.

• A path from s to t does not mean that there is path from t to s.

• (Weak) connectivity: If we ignored the directions for all edges, there would a path from any node to any node.

• Strong connectivity: For every two nodes u and v, there is a path from u to v and a path from v to u.

Mutual reachability (互相可达性)

• Two nodes u and v are mutually reachable, if there is path from u to v and a path from v to u in G.

• Strong connectivity: For every pair of nodes u and v, these nodes are mutually reachable.

• Transitivity: If u and v are mutually reachable and v and w are mutually reachable, then u and w are mutually reachable.

Testing strong connectivity

• Define the reverse graph Grev, in which the nodes are the same and the edges are the same with reversed directions.

• Pick any node s in V and run BFS(G,s) and BFS(Grev,s).

• If one of the two searches does not reach every node, then the graph is definitely not strongly connected.

• Assume that both searches reach every node. This means that there is a path from s to any node u and a path from any node u to s.

  • For any node u, s and u are mutually reachable.

• Pick any other node v. Since s and v are also mutually reachable, by transitivity, v and u are mutually reachable and the graph is strongly connected.

DAGs and Topological Ordering

Directed Acyclic Graphs

• Definition: A directed acyclic graph (DAG) G is a graph that does not have any cycles.

• Properties of DAGs

  • They appear frequently in applications.
  • Example - prerequisite modules: To take module A you need to have taken module B and module C.
  • If the module prerequisite relation has a cycle, then it is impossible to get a degree!

• Topological Ordering （拓扑排序）

• Given a directed graph G, a topological ordering of G is an ordering of the nodes u1, u2, … , un, such that for every edge e=(ui, uj), it holds that i < j.

• Intuitively, a topological ordering orders the nodes in a way such that all edges point “forward”.

• Topological Ordering implies DAG

  • If graph G has a topological ordering, then G is a DAG.

  • Suppose by contradiction that G has a topological ordering (u1, u2, … , un) but it also has a cycle C.

  • Let uj be the smallest element of C according to the topological ordering.

  • Let ui be its predecessor in the cycle (i.e., there is an edge e=(ui, uj)).

  • ui must appear before uj in the topological order (by the presence edge e).

  • This contradicts the fact that uj was the smallest element of C according to the topological ordering.

• TO(拓扑排序) => DAG(有向无环图) was proved via proof-by-contradiction.

• DAG => TO will be proved via “proof-by-algorithm”.

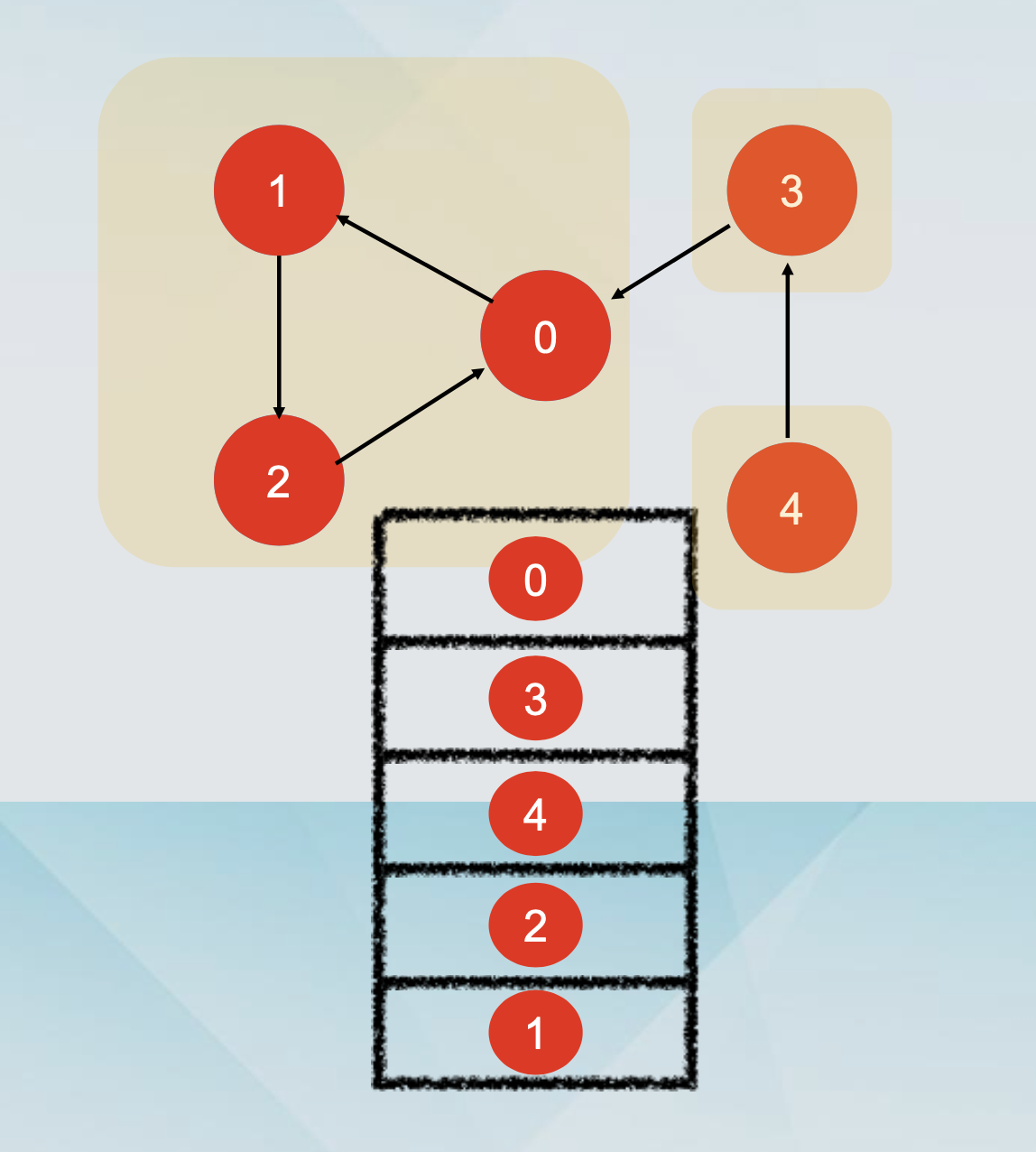
Source node

• The starting node must have no incoming edges!

• A source node is a node with no incoming edges(传入的边).

• Lemma: Every DAG has at least one source node. 所有 DAG 至少有一个 source node

• Proof by contradiction:

  • Assume that every node has at least one incoming edge.

  • Start from any node u and follow edges from u backwards.

    • Equivalently, we move to a neighbour of u in Grev.

  • We can do that for every node, since by assumption there is no source.

  • After at least n+1 steps, we will have visited the same node twice.

  • The graph has a cycle, therefore it can’t be a DAG. Contradiction!

• If we remove a node u and all its incident edges from a DAG G, the resulting graph G’ is still a DAG.

• If G’ had a cycle, the same cycle would be present in G.

DAG implies topological ordering

• Proof-by-induction:

  • Base Case: If the DAG has one or two nodes, it clearly has a topological ordering.

  • Inductive step: Assume that a DAG with up to k nodes has a topological ordering (Inductive Hypothesis). We will prove that a DAG with k+1 nodes has a topological ordering.

    • By our lemma, there is at least one source node in G, and let u be such a node.

    • Put u first in the topological ordering (safe, since u is a source).

    • Consider the graph G’, obtained by G if we remove u and its incident edges.

    • G’ is a DAG (by the simple fact) with k nodes.

      • It has a topological ordering by the induction hypothesis.

    • Append this ordering to u.

Proof-by-algorithm

/**
 * Algorithm TopologicalSort(G)
 *  Find a source vertex u and put it first in the order.
 *  Let G’=G-{u} TopologicalSort(G’) Append this order after u
 */

Running time

O(n^2)

Finding Strongly Connected Components

• A connected component of an undirected graph G is subgraph such that any two nodes are connected via some path.

• A strongly connected component of a directed graph G is subgraph such that any two nodes are mutually reachable.

How do we find all strongly connected components of a graph G?

• We can run the “forward” and “backward” BFS for a node s and find the set of nodes that are mutually reachable from s.

  • This is the strongly connected component of s.

  • But BFS might produce different connected components, depending on how we visit the nodes.

  • We need a consistent way of visiting them in the “forward” and in the “backward” pass.

Kosajaru’s algorithm

• Perform a DFS on G, starting from an arbitrary nodes s.

• Add the nodes that the DFS tree reaches to a stack.

  • A node is added to the stack when the DFS for that node is completed.

• Perform a DFS on Grev, visiting the nodes in the order that they are popped from the stack.

• Output the DFS trees of the second DFS as the strongly connected components.

Running time

The running time is O(m+n).

Correctness

Simple but key lemma

• Let C and C’ be distinct SCCs in a directed graph G. Let u, v in C Let u’,v’ in C’

  Suppose that G contains a path from u to u’. (1)

  Then G cannot contain a path from v’ to v.

• Proof (by contradiction):

  • Assume there is a path from v’ to v. (2)

  • There is a path from u’ to v’ (same SCC).

  • There is path from u to v’ (because of (1) and previous bullet).

  • There is a path from v to u (same SCC).

  • There is path from v’ to u (because of (2) and previous bullet).

  • This means that u and v’ are mutually reachable, hence in the same SCC.

• Lemma: Let C and C’ be distinct SCCs in G. Suppose there is a directed edge crossing from C to C’. Then the DFS on the nodes of C finishes later than the DFS on the nodes of C’.

Lemma and Corollary(推论)

• Lemma: Let C and C’ be distinct SCCs in G. Suppose there is a directed edge crossing from C to C’. Then the DFS on the nodes of C finishes later than the DFS on the nodes of C’.

• Corollary: If the forward DFS finishes on component C later than component C’, then

  • there is no edge crossing from C’ to C in G.

  • there is no edge crossing from C to C’ in Grev.

• This means that in the reverse DFS on Grev, if we start with the SCC that finishes last in the forward DFS of G, we will not find edges to other SCCs.